Toán 11 Kết nối tri thức Bài 20: Hàm số mũ và hàm số lôgarit
1.1. Hàm số mũ
a) Khái niệm
Cho a là số thực dương khác 1.
Hàm số \(y = a^x\) được gọi là hàm số mũ cơ số a.
b) Tính chất
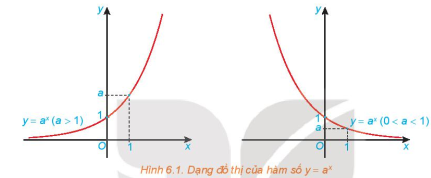
Hàm số mũ \(y = a^x\):
- Tập xác định: \(\mathbb{R}\) và tập giá trị: \((0;+\infty )\).
- Đồng biến trên \(\mathbb{R}\) khi \(a>1\) và nghịch biến trên \(\mathbb{R}\) khi \(0 < a < 1\).
- Liên tục trên \(\mathbb{R}\).
- Có đồ thị đi qua các điểm \((0;1), (1;a)\) và luôn nằm phía trên trục hoành.
1.2. Hàm số Lôgarit
a) Khái niệm
Cho a là số thực dương khác 1.
Hàm số \(y =\log_a x\) được gọi là hàm số lôgarit cơ số a.
b) Tính chất
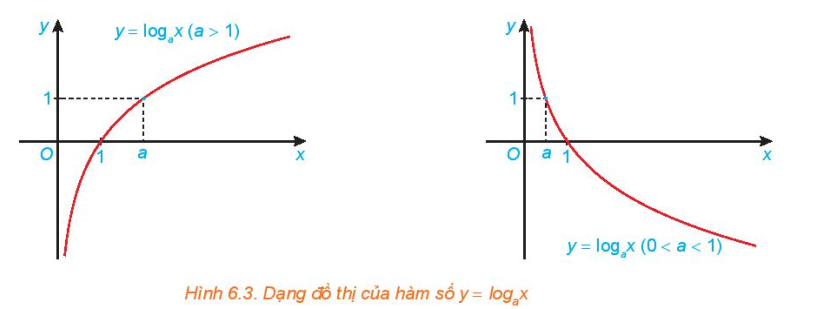
Hàm số mũ \(y =\log_a x\):
- Tập xác định: \((0;+\infty )\) và tập giá trị: \(\mathbb{R}.\)
- Đồng biến trên \((0;+\infty )\) khi \(a>1\) và nghịch biến trên \((0;+\infty )\) khi \(0 < a < 1\).
- Liên tục trên \((0;+\infty )\).
- Có đồ thị đi qua các điểm \((1; 0), (a; 1)\) và luôn nằm bên phải trục tung.