Toán 10 Kết nối tri thức Bài 11: Tích vô hướng của hai vectơ

Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) khác \({\vec 0}\). Từ một điểm A tuỳ ý, vẽ các vectơ \(\overrightarrow {AB}  = \overrightarrow u \) và \(\overrightarrow {AC}  = \overrightarrow v \) (Hình cho bên dưới). Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay đơn giản là góc giữa hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) kí hiệu là \(\left( {\overrightarrow u ,\overrightarrow v } \right)\).

Chú ý: 

+ Quy ước rằng góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow 0 \) có thể nhận một giá trị tuỳ ý từ 0° đến 180°.

+ Nếu \(\left( {\overrightarrow u ,\overrightarrow v } \right) = {90^0}\) thì ta nói rằng \(\overrightarrow u \) và \(\overrightarrow v \) vuông góc với nhau, kí hiệu là \({\overrightarrow u  \bot \overrightarrow v }\) hoặc \({\overrightarrow v  \bot \overrightarrow u }\). Đặc biệt \(\overrightarrow 0 \) được coi là vuông góc với mọi vectơ.

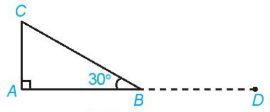
Ví dụ: Cho tam giác ABC vuông tại A và \(\widehat B = {30^0}\). Tính \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right),\left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\). 

Giải

Ta có: 

\(\begin{array}{l}
\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \overrightarrow {BAC}  = {90^0}\\
\left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = \widehat {ACB} = {60^0}\\
\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BD} ,\overrightarrow {BC} } \right) = \widehat {DBC} = {150^0}
\end{array}\) 

Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u .\overrightarrow v \), được xác định bởi công thức sau: \(\overrightarrow u .\overrightarrow v  = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.cos\left( {\overrightarrow u ,\overrightarrow v } \right)\)

Chú ý:

\(\overrightarrow u  \bot \overrightarrow v  \Leftrightarrow \overrightarrow u .\overrightarrow v  = \overrightarrow 0 \)

\(\overrightarrow u .\overrightarrow u \) còn được viết là \({\overrightarrow u ^2}\). Ta có \({\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.cos{0^0} = {\left| {\overrightarrow u } \right|^2}\) 

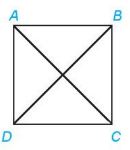
Ví dụ: Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng sau: \(\overrightarrow {AB} .\overrightarrow {AD} ,\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AB} .\overrightarrow {BD} \) 

Giải

Vì \(\left( {\overrightarrow {AB} .\overrightarrow {AD} } \right) = {90^0}\) nên \(\overrightarrow {AB} .\overrightarrow {AD}  = 0\).

Hình vuông có cạnh bằng a nên có đường chéo bằng \(a\sqrt 2 \) 

Mặt khác, \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = {45^0},\left( {\overrightarrow {AB} ,\overrightarrow {B{\rm{D}}} } \right) = {135^0}\), do đó \(\overrightarrow {AB} .\overrightarrow {AC}  = AB.AC.cos{45^0} = a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2}\), \(\overrightarrow {AB} .\overrightarrow {B{\rm{D}}}  = AB.B{\rm{D}}.cos{135^0} = a.a\sqrt 2 .\left( { - \frac{{\sqrt 2 }}{2}} \right) =  - {a^2}\) 

Tích vô hướng của hai vectơ \(\overrightarrow u  = \left( {x';y'} \right)\) được tính theo công thức: \(\overrightarrow u .\overrightarrow v  = xx' + yy'\)

Nhận xét: 

+ Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) vuông góc với nhau khi và chỉ khi xx' + yy' = 0.

+ Bình phương vô hướng của \(\overrightarrow u \left( {x;y} \right)\) là \({\overrightarrow u ^2} = {x^2} + {y^2}\). 

+ Nếu \(\overrightarrow u  \ne \overrightarrow 0 \) và \(\overrightarrow v  \ne \overrightarrow 0 \) thì \(cos\left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{x{\rm{x}}; + yy'}}{{\sqrt {{x^2} + {y^2}} .\sqrt {x{'^2} + y{'^2}} }}\) 

Tính chất của tích vô hướng  Với ba vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow {\rm{w}} \) bất kì và mọi số thực k. ta có: * \(\overrightarrow u .\overrightarrow v  = \overrightarrow v .\overrightarrow u \) (tính chất giao hoán); * \(\overrightarrow u .\left( {\overrightarrow v  + \overrightarrow {\rm{w}} } \right) = \overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow {\rm{w}} \) (tính chất phân phối đối với phép cộng); * \(\left( {k\overrightarrow u } \right).\overrightarrow v  = k\left( {\overrightarrow u .\overrightarrow v } \right) = \overrightarrow u \left( {k.\overrightarrow v } \right)\).

Chú ý: Từ các tính chất trên, ta có thể chứng minh được:

+ \(\vec u.\left( {\vec v - \overrightarrow {\rm{w}} } \right) = \vec u.\vec v - \vec u.\overrightarrow {\rm{w}} \) (tính chất phân phối đối với phép trừ)

+ \({\left( {\overrightarrow u  + \overrightarrow v } \right)^2} = {\overrightarrow u ^2} + 2\overrightarrow u .\overrightarrow v  + {\overrightarrow v ^2};{\left( {\overrightarrow u  - \overrightarrow v } \right)^2} = {\overrightarrow u ^2} - 2\overrightarrow u .\overrightarrow v  + {\overrightarrow v ^2}\) 

+ \(\left( {\overrightarrow u  + \overrightarrow v } \right).\left( {\overrightarrow u  - \overrightarrow v } \right) = \overrightarrow u  - \overrightarrow v \) 

Ví dụ: Trong mặt phẳng toạ độ Oxy, tính tích vô hướng của các cặp vectơ sau:

a) \(\overrightarrow u  = \left( {2; - 3} \right)\) và \(\overrightarrow v  = \left( {5;3} \right)\) 

b) Hai vectơ đơn vị \(\overrightarrow i \) và \(\overrightarrow j \) tương ứng của các trục Ox, Oy.

Giải

a) Ta có: \(\overrightarrow u .\overrightarrow v  = 2.5 + ( - 3).3 = 10 - 9 = 1\) 

b) Vì \(\overrightarrow i  = \left( {1;0} \right)\) và \(\overrightarrow i  = \left( {0;1} \right)\) nên \(\overrightarrow i .\overrightarrow j  = 1.0 + 0.1 = 0\)