2.1. Mặt nón – Hình nón – Khối nón
a) Mặt nón
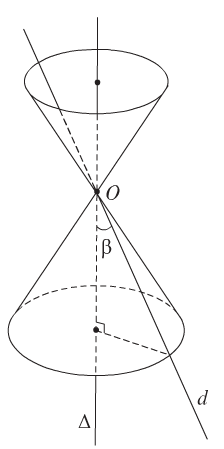
– Trong không gian cho hai đường thẳng \(\Delta\) và \(l\) cắt nhau tại O sao cho \((\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ}).\)
Cho \(l\) quay quanh \(\Delta\) ta được mặt nón tròn xoay có:
+ \(l\) là đường sinh.
+ \(\Delta\) trục của mặt nón.
+ \(O=l\cap \Delta\) đỉnh của mặt nón.
+ \(2\alpha :\) góc ở đỉnh.
b) Hình nón
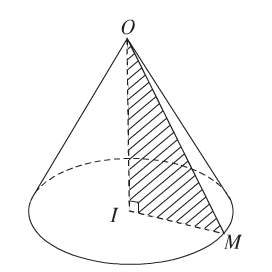
– Cắt mặt nón tròn xoay đỉnh O, trục \(\Delta\) bởi mặt phẳng (P) sao cho \((P)\perp \Delta ,O\notin (P).\)
– Hình giới hạn bởi mặt nón, mặt phẳng (P) được gọi là hình nón.
c) Khối nón
– Khối nón tròn xoay là phần không gian giới hạn bởi hình nón tròn xoay kể cả hình nón đó.
d) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón
– Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:
+ Thể tích khối nón: \(V_{Khoi \, \, non}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).
+ Diện tích xung quanh hình nón: \(S_{xq}=\pi Rl\).
+ Diện tích toàn phần hình nón: \(S_{tp}=\pi Rl+\pi R^{2}\).
2.2. Mặt trụ – Hình trụ – Khối trụ
a) Mặt trụ
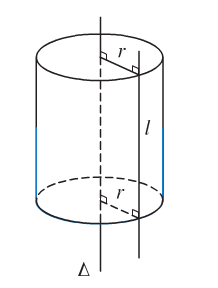
– Trong không gian, cho đường thẳng \(l\) song song và cách đường thẳng \(\Delta\) một khoảng R.
– Cho \(l\) quay quanh \(\Delta\) ta được một mặt tròn xoay được gọi là mặt trụ tròn xoay có:
+ \(l\) là đường sinh.
+ \(\Delta\) là trục mặt trụ.
+ R là bán kính mặt trụ.
b) Hình trụ
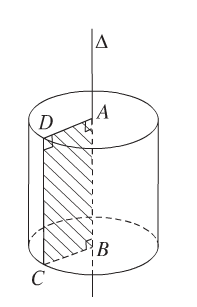
– Xét hình chữ nhật OABO’.
– Cho đường gấp khúc OABO’ quay quanh OO’ ta được hình trụ tròn xoay:
+ OA: Bán kính đường tròn đáy.
+ AB: đường sinh.
c) Khối trụ
– Khối trụ tròn xoay là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ đó.
d) Các công thức tính toán liên quan đển hình trụ, khối trụ
+ Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).
+ Diện tích xung quanh hình trụ: \(S_{xq}=2\pi .R.h\).
+ Diện tích toàn phân hình trụ: \(S_{tp}=2\pi .R.h+2\pi R^2\).
(Trong đó: R: bán kính đáy, h: chiều cao (k/c giữa hai đáy = OO’).)