2.1. Tính chất của thể tích khối đa diện
– Hai khối đa diện bằng nhau thì có thể tích bằng nhau.
– Nếu 1 khối đa diện được phân chia thành các khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ.
– Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1.
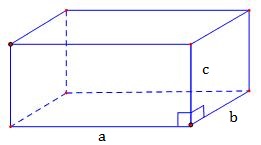
2.2. Thể tích khối hộp chữ nhật
– Giả sử có 1 khối hộp chữ nhật với 3 kích thước a, b, c đều là những số dương. Khi đó thể tích của nó là: \(V=a.b.c\).
2.3. Thể tích khối chóp
– Thể tích của 1 khối chóp bắng một phần ba tích số của mặt đáy và chiều cao khối chóp đó: \(V=\frac{1}{3}S_{day}.h.\)
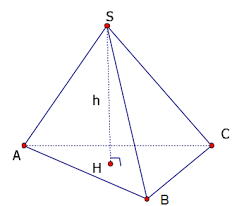
\(V_{S.ABCD}=\frac{1}{3}S_{ABC}.SH\)
– Công thức tỉ số thể tích của khối chóp tam giác:
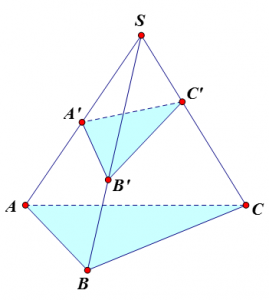
– Trên các đường thẳng SA, SB, SC của hình chóp S.ABC ta lấy lần lượt các điểm A’, B’, C’. Ta có: \({V_{S.A’B’C’}} = \frac{{SA;.SB’.SC’}}{{SA.SB.SC}}{V_{S.ABC}}\).
2.4. Thể tích khối lăng trụ
– Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy với chiều cao của khối lăng trụ đó: \(V=S_{day}.h.\)
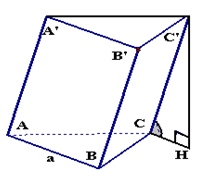
\(V_{ABC.A’B’C’}=S_{ABC}.C’H\)