2.1. Công thức mũ và lũy thừa
Cho a và b>0, m và n là những số thực tùy ý, ta có các công thức mũ và lũy thừa sau:

2.2. Công thức lôgarit
Cho \(a<0\ne1,b>0\) và \(x,y>0,\) ta có các công thức sau:

Công thức đổi cơ số:

2.3. Đạo hàm của hàm số lũy thừa, hàm số mũ và hàm số lôgarit

2.4. Hàm số lũy thừa, hàm số mũ, hàm số lôgarit
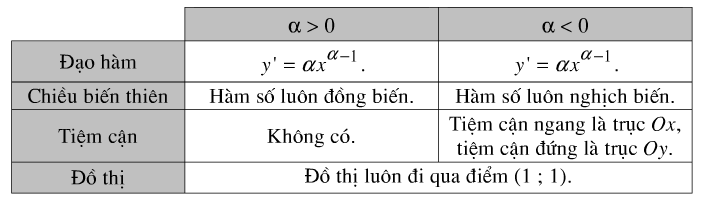
a) Hàm số lũy thừa
Bảng tóm tắt các tính chất của hàm số lũy thừa \(y=x^{\alpha}\) trên khoảng \(\left( {0; + \infty } \right)\)
b) Hàm số mũ
Bảng tóm tắt các tính chất của hàm số mũ \(y=a^x(a>0,a\ne1)\)

c) Hàm số lôgarit
Bảng tóm tắt các tính chất của hàm số lôgarit \(y={\log_a}x(a>0,a\ne1)\)

2.5. Phương trình và bất phương trình mũ
– Các phương pháp giải:
+ Phương pháp đưa về cùng cơ số.
+ Phương pháp lôgarit hóa.
+ Phương pháp đặt ẩn phụ.
+ Phương pháp hàm số.
2.6. Phương trình và bất phương trình lôgarit
– Các phương pháp giải:
+ Phương pháp đưa về cùng cơ số
+ Phương pháp mũ hóa.
+ Phương pháp đặt ẩn phụ.
Phương pháp hàm số.