2.1. Hàm số mũ
a) Định nghĩa hàm số mũ
– Cho số thực dương \(a\) khác 1.
– Hàm số \(y=a^x\) được gọi là hàm số mũ cơ số \(a\).
b) Tính chất hàm số mũ
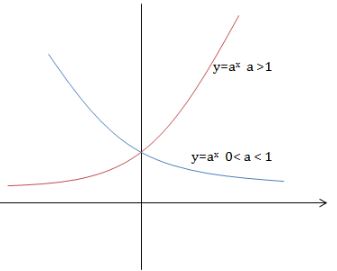
– Tập xác định: \(\mathbb{R}.\)
– Tập giá trị: \((0;+\infty )\)
– Với \(a>1\) hàm số \(y=a^x\) đồng biến trên \(\mathbb{R}.\)
– Với \(0 < a < 1\) thì hàm số luôn nghịch biến
– Đồ thị hàm số mũ nhận trục \(Ox\) làm tiệm cận ngang.
c) Đạo hàm của hàm số mũ
– Hàm số \(y=e^x\) có đạo hàm với mọi \(x\) và: \(\left ( e^x \right )’=e^x\)
– Hàm số \(y=a^x(a>0,a\ne 1)\) có đạo hàm tại mọi \(x\) và: \(\left( {{a^x}} \right)’ = {a^x}{\mathop{\rm lna}\nolimits}\)
– Đối với hàm hợp:
+ \(({e^u})’ = u’.{e^u}\)
+ \(({a^u})’ = {a^u}.\ln a.u’\)
2.2. Hàm số Lôgarit
a) Định nghĩa hàm số Lôgarit
– Cho số thực dương \(a\) khác 1.
– Hàm số \(y=\log_ax\) được gọi là hàm số lôgarit cơ số \(a.\)
b) Tính chất hàm số Lôgarit
– Tập xác định: \(\left( {0; + \infty } \right).\)
– Tập giá trị: \(\mathbb{R}.\)
– Với \(a>1\): \(y=\log_ax\) là hàm số đồng biến trên \(\left( {0; + \infty } \right).\)
– Với \(0< a < 1\) thì hàm số luôn nghịch biến
– Với \(x_1>0,x_2>0\): \(\log_ax_1=\log_ax_2\Leftrightarrow x_1=x_2\)
c) Đạo hàm của hàm số logarit
– Đạo hàm:
+ \(\left( {{{\log }_a}x} \right)’ = \frac{1}{{x\ln a}}\)
+ \(\left( {{{\log }_a}\left| x \right|} \right)’ = \frac{1}{{x\ln a}}\)
+ \(\left( {\ln x} \right)’ = \frac{1}{x}\)
– Đối với hàm hợp:
+ \(\left( {{{\log }_a}u} \right)’ = \frac{{u’}}{{u.\ln a}}\)
+ \(\left( {\ln u} \right)’ = \frac{{u’}}{{\ln u}}\)