Giả sử một công việc có thể được thực hiện theo phương án A hoặc phương án B. Phương án A có m cách thực hiện, phương án B có n cách thực hiện không trùng với bất kì cách nào của phương án A. Khi đó, công việc có thể thực hiện theo m + n cách.

Ví dụ: Lớp 10A có 36 học sinh, lớp 10B có 40 học sinh. Có bao nhiêu cách cử một học sinh của lớp 10A hoặc của lớp 10B tham gia một công việc tình nguyên sắp điễn ra?

Giải

Công việc cử một học sinh có hai phương ản thực hiện:

Phương án 1: Cử một học sinh của lớp 10A, có 36 cách thực hiện.

Phương án 2: Cử một học sinh của lớp 10B, có 40 cách thực hiện.

Ta thây mỗi cách thực hiên của phương án này không trùng với bất kì cách nào của phương ản kia. Do đó, theo quy tác công. cỏ 36 + 40 = 76 cách cử một học sinh thuộc một trong hai lớp tham gia công việc tình nguyên.

Mở rộng hơn, trong ví dụ sau đây, ta xét công việc có ba phương án thực hiện.

Giả sử một công việc được chúa thành hai công đoạn. Công đoạn thứ nhât có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn thứ hai. Khi đó, công việc có thể thực hiện theo m.n cách.

Ví dụ 1: Có ba thị trấn A, B, C. Có 5 con đường đề đi từ A đến B; có 3 con đường để đi từ B đến C. Có bao nhiêu cách chọn một con đường để đi từ A, qua B rồi đến C?

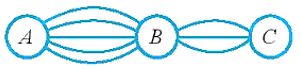
Giải

Việc đi từ A, qua B rồi đền C gồm 2 công đoạn:

Công đoạn thứ nhất: Đi từ A đến B, có 5 cách chọn đường đi

Công đoạn thứ hai: Ứng với mỗi cách chọn đường đi từ A đến B, có 3 cách chọn đường đi từ B tới C.

Theo quy tắc nhân, có 5.3 = 15 cách chọn đường đề đi từ A, qua B rồi đến C.

Ví dụ 2:

Từ năm chữ số 0, 1, 2, 3, 4, có thể lập được bao nhiêu

a) số tự nhiên có ba chữ sô đôi một khác nhau?

b) số tự nhiên chẵn có ba chữ số đôi một khác nhau?

Giải

Kí hiệu số cần lập là \(\overline {abc} \), với a, b, e là ba chữ số đôi một khác nhau từ các chữ số đã cho.

a) Có 4 cách lựa chọn chữ số a từ bồn chữ số khác 0 đã cho.

Ứng với mỗi cách chọn đó, có 4 cách chọn chữ số b từ bôn chữ số còn lại.

Ứng với mỗi cách chọn đó, có 3 cách chọn chữ số c từ ba chữ số còn lại.

Từ đó, áp dụng quy tắc nhân, có 4 . 4 . 3 = 48 số tự nhiên có ba chữ số đôi một khác nhau lập được tử các chữ sô đã cho.

b) Để số \(\overline {abc} \) là số chẵn, chữ số c phải là chữ số chẵn. Ta xét hai trường hợp sau đây.

* Trường hợp 1: c = 0. Khi đó, có 4 cách chọn chữ số a từ bôn chữ số còn lại, và ứng với mỗi cách chọn đó, có 3 cách chọn chữ số b từ ba chữ sô còn lại. Do đó, theo quy tắc nhân, trường hợp này có 4. 3 = 12 số thoả mãn yêu cầu.

* Trường hợp 2: c = 2 hoặc c = 4. Khi đó, có hai cách chọn chữ số c từ hai chữ sô 2 hoặc 4. Ứng với mỗi cách chọn đó, có 3 cách chọn chữ số a từ ba chữ số khác 0 còn lại, và ứng với mỗi cách chọn đó, có 3 cách chọn chữ sô b từ các chữ số còn lại. Do đó, theo quy tắc nhân, trường hợp này có 2. 3. 3= 18 số thoả mãn yêu cầu.

Trong hai trường hợp trên, mỗi số lập được theo trường hợp này đều khác với các số lập được của trường hợp kia. Theo quy tắc cộng, có 12 + 18 = 30 số tự nhiên chẵn có ba chữ số đôi một khác nhau lập được từ các chữ số đã cho.