1.1. Hàm số mũ
Cho a là số thực dương khác 1.
Hàm số \(y = a^x\) được gọi là hàm số mũ cơ số a.
Đồ thị của hàm số mũ
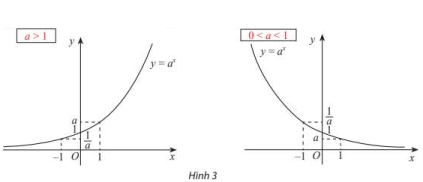
(1) Tập xác định: \(D=\mathbb{R}\).
Tập giá trị: \(T = (0;+\infty )\).
Hàm số liên tục trên \(\mathbb{R}\).
(2) Sự biến thiên:
Nếu \(a>1\) thì hàm số đồng biến trên \(\mathbb{R}\) và
\[\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {a^x} = + \infty ,\\
\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {a^x} = 0.
\end{array}\]
Nếu \(0 < a < 1\) thì hàm số nghịch biến trên \(\mathbb{R}\) và
\[\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {a^x} = 0 ,\\
\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {a^x} = + \infty.
\end{array}\]
(3) Đồ thị: cắt trục tung tại điểm \((0;1)\); đi qua điểm \((1;a)\) và luôn nằm phía trên trục hoành.
1.2. Hàm số lôgarit
Cho a là số thực dương khác 1.
Hàm số \(y =\log_a x\) được gọi là hàm số lôgarit cơ số a.
Đồ thị của hàm số lôgarit
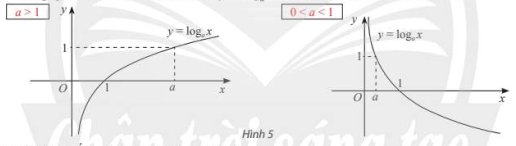
(1) Tập xác định: \(D=(0;+\infty )\).
Tập giá trị: \(T = \mathbb{R}\).
Hàm số liên tục trên \((0;+\infty )\).
(2) Sự biến thiên:
Nếu \(a>1\) thì hàm số đồng biến trên \((0;+\infty )\) và
\[\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {\log _a}x = + \infty ,\\
\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x = – \infty .
\end{array}\]
Nếu \(0 < a < 1\) thì hàm số nghịch biến trên \((0;+\infty )\) và
\[\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {\log _a}x = – \infty ,\\
\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} {\log _a}x = + \infty .
\end{array}\]
(3) Đồ thị: cắt trục tung tại điểm \((1;0)\); đi qua điểm \((a;1)\) và luôn nằm bên phải trục tung.