1.1. Vị trí tương đối của hai đường thẳng trong không gian
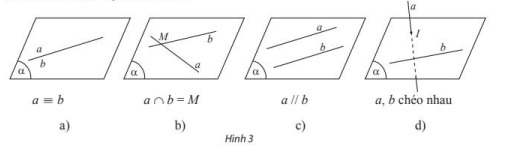
– Trường hợp 1: Có một mặt phẳng chứa a và b. Khi đó ta nói a và b đồng phẳng. Theo kết quả của hình học phẳng, có ba khả năng sau đây xảy ra
• Nếu a và b có hai điểm chung thì ta nói a trùng ở, kí hiệu a \(\equiv\) b.
• Nếu a và b có một điểm chung duy nhất M thì ta nói a và b cắt nhau tại M, kí hiệu a\(\cap\)b = M.
• Nếu a và b không có điểm chung thì ta nói a và b song song với nhau, kí hiệu a // b.
– Trường hợp 2: Không có mặt phẳng nào chứa cả a và b. Khi đó ta nói hai đường thẳng a và b chéo nhau hay a chéo với b.
Hai đường thẳng gọi là song song nếu chúng nằm trong cùng một mặt phẳng và không có điểm chung.
Chú ý:
+) Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.
+) Cho hai đường thẳng song song a và b. Có duy nhất một mặt phẳng chứa hai đường thắng đó, kí hiệu mp(a, b).
1.2. Tính chất cơ bản về hai đường thẳng song song
Định lý 1:
Trong không giản, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thăng đó.
Định lý 2:
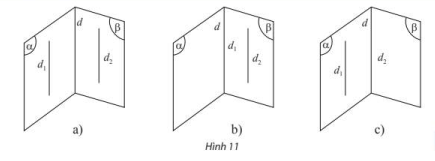
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thi ba giao tuyển ấy hoặc đồng quy hoặc đội một song song.
Hệ quả:
Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Định lý 3:
Hai đường thẳng phân biệt cùng song song với một dường thẳng thứ ba thì song song với nhau.
Chú ý: Khi hai đường thẳng phân biệt a, b cùng song song với đường thẳng c thì ta có thể kí hiệu là a // b // c và gọi là ba đường thẳng song song.