1.1. Phương trình tương đương
|
– Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm. |
1.2. Phương trình sin x = m
|
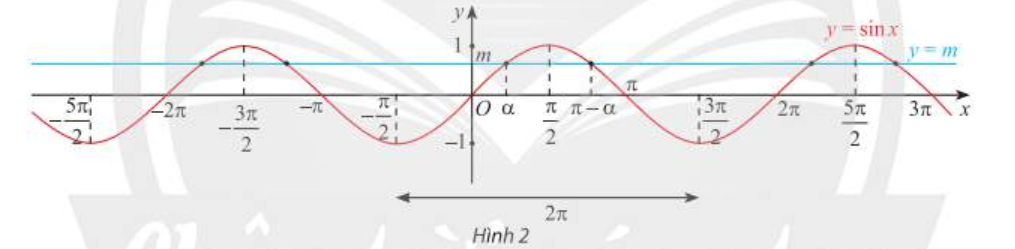
Xét phương trình sin x = m. – Nếu |m| > 1 thì phương trình vô nghiệm. – Nếu |m| ≤ 1 thì phương trình có nghiệm: \(\left[ \begin{array}{l} x = \alpha + k2\pi \\ x = \pi – \alpha + k2\pi \end{array} \right. (k\in Z)\) với \(\alpha \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho sin \(\alpha \) = m. |
Chú ý
– Một số trường hợp đặc biệt.
|
\(\sin x = 0 \Leftrightarrow x = k\pi ,(k \in Z)\\ \sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,(k \in Z)\\ \sin x = – 1 \Leftrightarrow x = – \frac{\pi }{2} + k2\pi ,(k \in Z)\) |
– Hơn nữa ta có:
| \(\begin{array}{l} \sin u = \sin v \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} u = v + k2\pi\\ u = \pi – v + k2\pi \end{array} \right.(k \in Z) \end{array}\) |
– Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \(\begin{array}{l} \sin x = \sin \alpha \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} x = {\alpha ^0} + k{360^0}\\ x = 180 ^0 – {\alpha ^0} + k{360^0} \end{array} \right.(k \in Z) \end{array}\) |
1.3. Phương trình cos x = m
|
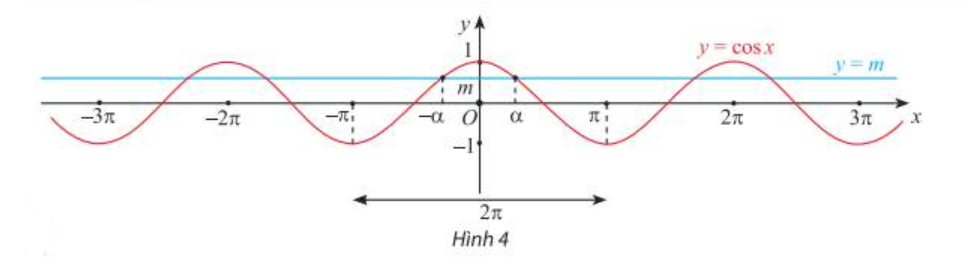
Xét phương trình cos x = m. – Nếu |m| > 1 thì phương trình vô nghiệm. – Nếu |m| ≤ 1 thì phương trình có nghiệm: \(\left[ \begin{array}{l} x = \alpha + k2\pi \\ x = – \alpha + k2\pi \end{array} \right. (k\in Z)\) với \(\alpha \in \left[ {0;{\pi }} \right]\) sao cho cos \(\alpha \) = m. |
Chú ý
– Một số trường hợp đặc biệt.
|
\(\cos x = 0 \Leftrightarrow x = k\pi ,(k \in Z)\\ \cos x = 1 \Leftrightarrow x = k2\pi ,(k \in Z)\\ \cos x = – 1 \Leftrightarrow x = {\pi } + k2\pi ,(k \in Z)\) |
– Hơn nữa ta có:
| \(\begin{array}{l} \cos u = \cos v \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} u = v + k2\pi\\ u = – v + k2\pi \end{array} \right.(k \in Z) \end{array}\) |
– Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \(\begin{array}{l} \cos x = \cos \alpha \\ \Leftrightarrow {\rm{ }}\left[ \begin{array}{l} x = {\alpha ^0} + k{360^0}\\ x = -{\alpha ^0} + k{360^0} \end{array} \right.(k \in Z) \end{array}\) |
1.4. Phương trình tan x = m
|
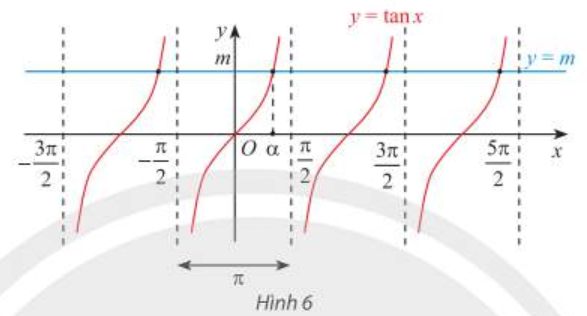
– Với mọi số thực m, phương trình tan x = m có nghiệm \(x = \alpha + k\pi \quad (k\in Z)\) với \(\alpha \in \left( {-{\pi \over 2};{\pi \over 2}} \right)\) sao cho tan \(\alpha \) = m. |
Chú ý
– Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \( \tan x = \tan \alpha \Leftrightarrow {\rm{ }} x = {\alpha ^0} + k{180^0}(k \in Z) \) |
1.5. Phương trình cot x = m
|
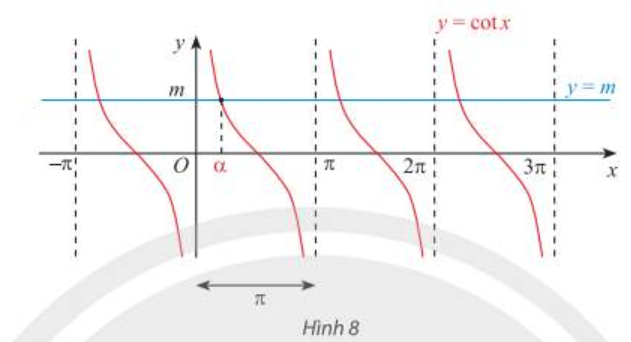
– Với mọi số thực m, phương trình cot x = m có nghiệm \(x = \alpha + k\pi \quad (k\in Z)\) với \(\alpha \in \left( {0;{\pi }} \right)\) sao cho cot \(\alpha \) = m. |
Chú ý
– Nếu số đo của góc \(\alpha \) được cho bằng đơn vị độ thì
| \( \cot x = \cot \alpha \Leftrightarrow {\rm{ }} x = {\alpha ^0} + k{180^0}(k \in Z) \) |