Bài toán gốc: Cho trước dãy số A: A[0], A[ 1], …, A[n-1]. Cần tiến hành sắp xếp dãy phải nhận được là trên theo thứ tự tăng dần. Kết quả phải nhận được:

A[0] ≤ A[1] ≤ … ≤ A[n-1]

Ví dụ: Với bộ dữ liệu đầu vào là dãy [2, 1,7,10,4] thì kết quả thu được dãy [1,2,4,7,10]. Quá trình phân tích, thiết kế được mô tả theo các bước sau.

Bài toán gốc là cho trước dãy A, cần sắp xếp lại dãy này theo thứ tự tăng dần. 

 

Việc thiết kế chương trình giải bài toán được chia thành nhiều bước:

– Bước 1: Thiết lập ý tưởng thiết kế ban đầu.

 + Ý tưởng ban đầu của thuật toán là duyệt từ phần tử thứ hai đến phần tử cuối của dãy để sắp xếp dãy.

 + Sử dụng vòng lặp với biến i chạy từ chỉ số 1 đến n-1.

 + Thực hiện các thao tác để bổ sung A[i] vào dãy các phần tử đã được sắp xếp A[0], A[1]…, A[i-1].

– Bước 2: Thực hiện việc “Chèn A[i] vào đúng vị trí.”D

+ Lấy phần tử A[i] ra và chuyển các phần tử bên trái A[i] nhưng có giá trị lớn hơn A[i] sang phải.

+ Đặt A[i] vào vị trí trống.

– Bước 3: Nhấc A[i] lên bằng cách tạo biến value để lưu trữ giá trị A[i].

value = A[ i ]

– Bước 4: Chuyển các phần tử bên trái A[i] và lớn hơn A[i] sang phải.

 + Thiết lập biến j = i – 1 là chỉ số của phần tử ngay bên trái A[i].

 + Liên tục so sánh A[j] với value, nếu A[j] > value thì chuyển A[j] sang phải một vị trí bằng lệnh A[j+1] = A[j] và giảm j = j – 1.

 + Quá trình kết thúc khi đi hết bên trái của dãy hoặc A[j] <= value.

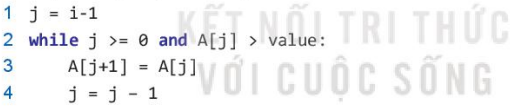
– Bước 5: Chèn A[i] vào đúng vị trí trống.

+ Vị trí j+1 là vị trí trống cần chèn.

+ Chèn phần tử A[i] (giá trị được lưu trong value) vào vị trí j+1 bằng câu lệnh A[j+1] = value.

Quá trình thiết kế kết thúc sau khi chi tiết hoá bằng các câu lệnh tất cả các thao tác được mô tả trong các bước trên.

 

Chương trình giải bài toán đặt ra được thiết kế hoàn chỉnh dưới dạng hàm InsertionSort(A). Tổng hợp các bước trên chúng ta có chương trình hoàn chỉnh như sau:

Quá trình thiết kế chương trình sắp xếp chèn đã trải qua nhiều bước, mỗi bước làm mịn dần các phân tích của bước trước đó.

 

Bài toán: Cho trước dãy số A: A[0], A[ 1], …, A[n-1]. Cặp phần tử A[i], A[j] được gọi là nghịch đảo nếu i < j nhưng A[i] > A[j]. Cần viết chương trình đếm số các cặp nghịch đảo của dãy A. Ví dụ dãy 3, 4, 2, 1 sẽ có 5 cặp nghịch đảo là (3,2), (3, 1), (4,2), (4,1), (2,1).

Thiết kế theo phương pháp làm mịn dần

Bài toán gốc là cho trước dãy số A có n phần tử, cần đếm số các cặp phần tử nghịch đảo của A.

 

Chúng ta sẽ thiết kế lời giải bài toán theo phương pháp làm mịn dần.

– Bước 1: Thiết lập ý tưởng thiết kế ban đầu.

 + Bài toán đếm các cặp chỉ số nghịch đảo của dãy A.

 + Chương trình sẽ trả về số lượng các cặp số nghịch đảo.

 + Cần tìm tất cả các cặp chỉ số (i, j) có thể tạo cặp nghịch đảo A[i], A[j], sau đó kiểm tra xem cặp này có là nghịch đảo không.

 

– Bước 2: Tìm tất cả các cặp chỉ số (ij).

 + Thiết lập 2 vòng lặp theo i, j để tìm.

 + Tìm các chỉ số i chạy từ 0 đến n-2, chỉ số j chạy từ i+1 đến n-1 để tiết kiệm thời gian.

– Bước 3: Kiểm tra tính nghịch đảo của cặp (i)).

 + Cặp (i, j) sẽ là nghịch đảo khi A[i] > A[j].

 + Điều kiện i < j đã được đảm bảo tại bước 2.

 

Trên cơ sở các phân tích trên chúng ta có thể thiết lập hàm Nghichdao(A) để đếm số các cặp nghịch đảo của dãy A cụ thể như sau: