– Động năng của vật dao động điều hòa được xác định bởi biểu thức

\({{\rm{W}}_d} = \frac{1}{2}m{\omega ^2}({A^2} – {x^2})\)

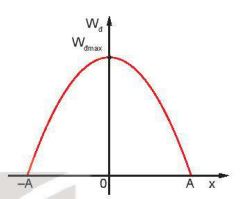
Hình 5.1. Sự biến thiên của động năng W_đ theo li độ x

– Đồ thị cho thấy, khi vật đi từ VTCB tới vị trí biên thì động năn của vật đang từ cực đại giảm đến 0. Khi vật đi từ vị trí biên về VTCB thì động năng của vật tăng từ 0 đến giá trị cực đại.

– Theo định luật bảo toàn năng lượng, nếu bỏ qua ma sát thì động năng của vật không mất đi mà chuyển dần thành thế năng của vật và ngược lại nên ta có:

\({{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{x^2}\)

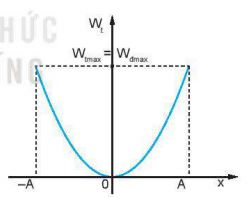
Hình 5.2. Sự biến thiên của động năng W_t theo li độ x

– Đồ thị biến thiên thế năng theo li độ x cũng là một đường Parabol nhưng bề lõm hướng lên như hình 5.2 và có giá trị cực đại:

\({{\rm{W}}_{t\max }}{\rm{ = }}{{\rm{W}}_{d\max }} = \frac{1}{2}m{\omega ^2}{A^2}\)

Trong dao động điều hòa, có sự chuyển hóa qua qua lại giữa động năng và thế năng của vật, còn cơ năng, tức tổng động năng và thế năng thì được bảo toàn

\(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\)

1.4.1. Con lắc lò xo

Hình 5.3. Con lắc lò xo

– Nếu bỏ qua ma sát thì dao động của con lắc lò xo là dao động điều hòa

– Chọn mốc thế năng ở VTCB thì thế năng của con lắc lò xo khi ở li độ x là:

\({{\rm{W}}_t} = \frac{1}{2}k{x^2}\)

Với k là độ cứng lò xo

Ta có: \(\omega  = \sqrt {\frac{k}{m}} \) và chu kì của con lắc lò xo là: \(T = 2\pi \sqrt {\frac{m}{k}} \)

– Cơ năng của con lắc lò xo: \(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\) = hằng số.

1.4.2. Con lắc đơn

– Vị trí của con lắc đơn được xác định bằng li độ dài s hay li độ góc \(\alpha \)

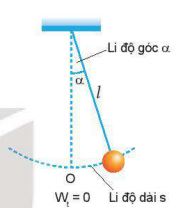
Hình 5.4. Con lắc đơn

– Thế năng của con lắc đơn là thế năng trọng trường. Chọn mốc thế năng ở VTCB thì thế năng của con lắc ở li độ góc \(\alpha \) là: 

\({{\rm{W}}_t} = mgl\frac{{{\alpha ^2}}}{2} = \frac{1}{2}m\frac{g}{l}{s^2}\)

– Ta có: \(\omega  = \sqrt {\frac{g}{l}} \)

– Tương tự với con lắc lò xo ta có: \(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\) = hằng số.

Một vật có khối lượng m dao động điều hòa với tần số góc \(\omega \) và biên độ A. Tại li độ x: – Động năng của vật là: \({{\rm{W}}_d} = \frac{1}{2}m{\omega ^2}({A^2} – {x^2})\) – Thế năng của con lắc là: \({{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{x^2}\) – Cơ năng của con lắc là: \(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\) = hằng số