– Li độ: x là độ dịch chuyển từ VTCB đến vị trí của vật tại thời điểm t

– Biên độ: A là độ dịch chuyển cực đại của vật tính từ VTCB

– Chu kì: T là khoảng thời gian để vật thực hiện được một dao động

– Tần số: f là số dao động mà vật thực hiện được trong một giây

\(f = \frac{1}{T}\)

Đơn vị của tần số: \(\frac{1}{s}\), gọi là Héc (Kí hiệu Hz)

– Tần số góc: ω

\(\omega T = 2\pi \) hay \(\omega  = \frac{{2\pi }}{T}(rad/s)\)

– Biên độ, chu kì, tần số và tần số góc là những đại lượng không đổi, không phụ thuộc vào thời điểm quan sát. Với các vật khác nhau thì các đại lượng này khác nhau. Vì thế chúng là những đại lượng đặc trưng cho dao động điều hòa.

1.2.1. Pha ban đầu.

.

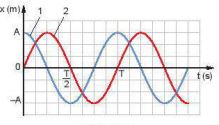
Hình 2.1

Hình 2.1 là đồ thị của hai vật dao động điều hoà cùng chu kì, cùng biên độ nhưng dao động 1 luôn đạt tới giá trị cực đại sớm hơn dao động 2 một thời gian là \(\frac{T}{4}\).

Từ đồ thị ta thấy, tại thời điểm ban đầu (t = 0) vật dao động điều hoà 1 đang ở vị trí biên x = A và sẽ dịch chuyển về VTCB, còn vật dao động điều hoà 2 đang ở VTCB và sẽ dịch chuyển về phía x>0.

Các phương trình dao động tương ứng với đồ thị Hình 2.1 có pha ban đầu \(\varphi \) lần lượt là:

                    \({x_1} = A\cos (\omega t)\) với \({\varphi _1} = 0\)

                    \({x_2} = A\cos (\omega t – \frac{\pi }{2})\) với \({\varphi _2} =  – \frac{\pi }{2}\)

Như vậy:

– Pha ban đầu \(\varphi \) cho biết tại thời điểm bắt đầu quan sát vật dao động điều hòa ở đâu và sẽ đi về phía nào.

– Pha ban đầu có giá trị nằm trong khoảng từ -\(\pi \) đến \(\pi \)

1.2.2. Độ lệch pha giữa hai dao động cùng chu kì.

Đồ thị Hình 2.1 còn cho thấy tại bất kì thời điểm nào thì độ lệch pha giữ hai dao động trên cũng bằng \(\frac{\pi }{2}\)

– Độ lệch pha là đại lượng không đổi, không phụ thuộc vào thời điểm quan sát.

\({\varphi _1} > {\varphi _2}\)${\mathrm{}}_{}$ thì dao động 1 sớm pha hơn dao động 2

\({\varphi _1} < {\varphi _2}\) thì dao động 1 trễ pha hơn dao động 2

\({\varphi _1} = {\varphi _2}\)${\mathrm{}}_{}$ thì dao động 1 cùng (đồng) pha với dao động 2

\({\varphi _1} = {\varphi _2} + \pi \) thì dao động 1 ngược pha với dao động 2

Ví dụ 1: Đồ thị li độ – thời gian của một vật dao động điều hòa được mô tả trên Hình 2.2.

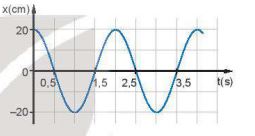
Hình 2.2

a, Xác định biên độ, chu kì, tần số, tần số góc, pha ban đầu và viết phương trình dao động.

b, Xác định pha của dao động tại thời điểm t = 2,5 s.

Giải:

a, Từ đồ thị ta xác định được:

Biên độ: A = 20 cm; chu kì T = 2,5 -0,5 = 2,0 s.

Áp dụng công thức: 

\(\omega  = \frac{{2\pi }}{T} = 2\pi f \Rightarrow \omega  = \pi (rad/s);f = 0,5Hz.\)

Khi \(t = 0,x = A\cos \varphi  \Rightarrow \cos \varphi  = 1 \Rightarrow \varphi  = 0(rad)\)

Do đó phương trình dao động của vật được viết: x = 20cos(t) (cm).

b, Từ phương trình dao động ta có:

\(\varphi  = \pi t + \frac{\pi }{2}\), thay t = 2,5 s vào suy ra \(\varphi  = 3\pi (rad)\)

Ví dụ 2: Hai vật dao động điều hòa A và B có cùng tần số nhưng lệch pha nhau được mô tả trên Hình 2.3.

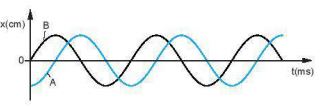
Hình 2.3

a, Xác định li độ của B khi A có li độ cực đại.

b, Xác định li độ của A khi B có li độ cực đại.

c, Xác định li độ của A khi B có li độ cực đại trước ( không kế thời điểm t = 0).

Giải:

Từ đồ thị, cho thấy:

a, Khi A có li độ cực đại thì B có li độ x = 0.

b, Khi B có li độ cực đại thì A có li độ x = 0.

c, A có li độ cực đại trước B.

d, Dao động A sớm pha \(\frac{\pi }{2}\) so với dao động B.

– Chu kì T là khoảng thời gian để vật thực hiện một dao động. Đơn vị của chu kì là giây (s). – Tần số f là số dao động mà vật thực hiện được trong một giây. Đơn vị của tần số là một trên giây (1/s), gọi là héc (kí hiệu là Hz). – Trong dao động điều hòa, giữa tần số góc \(\omega \), chu kì T và tần số f có mối liên hệ: \(\omega  = \frac{{2\pi }}{T} = 2\pi f\). Đơn vị của tần số góc là radian trên giây (rad/s). – Độ lệch pha giữa hai dao động điều hòa cùng chu kì luôn bằng độ lệch pha ban đầu.