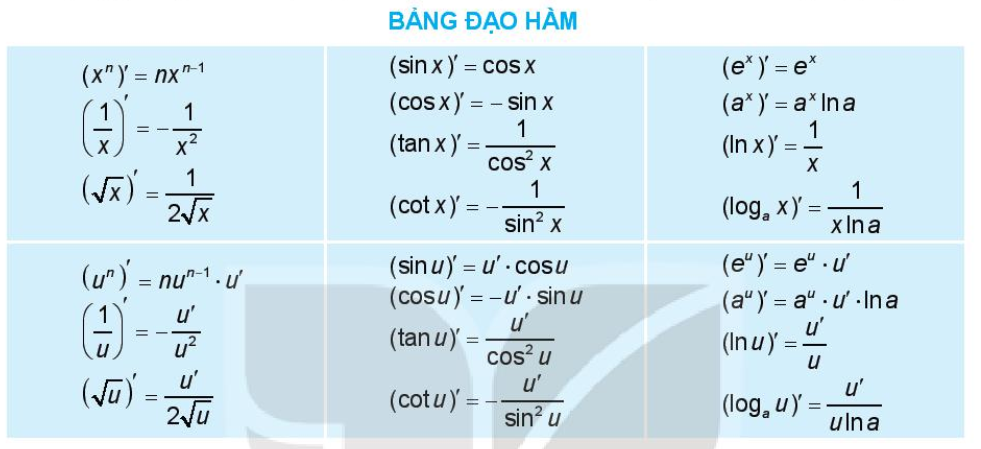
1.1. Đạo hàm của một số hàm số thường gặp
a) Đạo hàm của hàm số y = \(x^n\) (n \(\in\) N)
\[{\left( {{x^n}} \right)’} = n{x^{n – 1}}, x\in R.\]
b) Đạo hàm của hàm số y = \(\sqrt x\)
1.2. Đạo hàm của tổng, hiệu, tích, thương
Giả sử \(u = u\left( x \right)\) và \(v = v\left( x \right)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng (a; b). Ta có:
+ \({\left( {u + v} \right)’} = {u’} + {v’}\)
+ \({\left( {u – v} \right)’} = {u’} – {v’}\)
+ \({\left( {u.v} \right)’} = {u’}.v + u.{v’}\)
+ \(\left ( \frac{u}{v} \right )’=\frac{u’v-uv’}{v^2}, (v(x) \ne 0)\)
Chú ý:
– \({\left( {\frac{1}{v}} \right)’} = – \frac{{ – v’}}{{{v^2}}}\) , \((v(x)\ne 0)\)
1.3. Đạo hàm của hàm số hợp
a) Khái niệm hàm số hợp
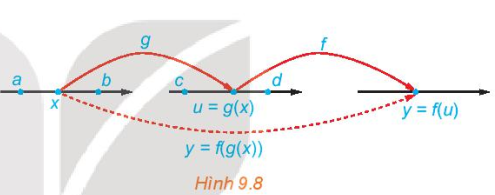
Giả sử u = g(x) là hàm số xác định trên khoảng (a; b), có tập giá trị chứa trong khoảng (c, d) và y = f(u) là hàm số xác định trên khoảng (c; d). Hàm số y = f(g(x)) được gọi là hàm số hợp của hàm số y = f(u) với u = g(x).
b) Đạo hàm của hàm số hợp
Nếu hàm số u = g(x) có đạo hàm \(u’_x\) tại x và hàm số y = f(u) có đạo hàm \(y’_u\) tại u thì hàm số hợp y = f(g(x)) có đạo hàm \(y’_x\) tại x là
1.4. Đạo hàm của hàm số lượng giác
a) Đạo hàm của hàm số y = sin x
Hàm số y = sinx có đạo hàm trên R và (sin x)’ = cos x.
Đối với hàm số hợp y = sinu, với u = u(x), ta có (sinu)’ = u’. cosu.
b) Đạo hàm của hàm số y = cos x
Hàm số y = cosx có đạo hàm trên R và ( cos x )’ = – sin x.
Đối với hàm số hợp y = cosu, với u = u(x), ta có: (cosu)’ =–u’. sinu.
c) Đạo hàm của các hàm số y= tan x và y = cot x
1.5. Đạo hàm của hàm số mũ và hàm số lôgarit
a) Giới hạn liên quan đến hàm số mũ và hàm số lôgarit
\(\begin{array}{l} \mathop {\lim }\limits_{x \to 0} {\left( {1 + x} \right)^{\frac{1}{x}}} = e;\\ \mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{x} = 1;\\ \mathop {\lim }\limits_{x \to 0} \frac{{{e^x} – 1}}{x} = 1. \end{array}\)
b) Đạo hàm của hàm số mũ
\(\begin{array}{l} \left( {{e^x}} \right)’ = {e^x}, \text{với mọi }x \in R \\ \Rightarrow \left( {{e^u}} \right)’ = u’.{e^u}\\ \left( {{a^x}} \right)’ = {a^x}\ln a,\,\text{với mọi }0 < a \ne 1,\,x \in R \\ \Rightarrow \left( {{a^u}} \right)’ = u’.{a^u}.\ln a \end{array}\)
c) Đạo hàm của hàm số lôgarit
Chú ý:
\[\left( {\ln \left| x \right|} \right)’ = \frac{1}{x}, \text{với mọi } x\ne 0.\]
Như vậy, chúng ta có bảng đạo hàm cho các hàm cơ bản như sau: