1.1. Góc giữa hai vectơ
|
Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( {\;\overrightarrow u ,\overrightarrow v } \right)\) *Cách xác định góc Chọn điểm A bất kì, vẽ \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\). |
|---|
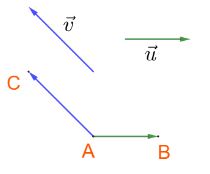
* Các trường hợp đặc biệt:
+) \(\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha \le {180^ \circ }\)
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v \) hoặc \(\overrightarrow v \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0 \bot \overrightarrow u \;\;\forall \overrightarrow u \;\)
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng
Chú ý:
– Từ định nghĩa ta có \(\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right)\)
– Góc giữa hai vectơ cùng hướng và khác \({\overrightarrow 0 }\) luôn bằng 00
– Góc giữa hai vectơ ngược hướng và khác \({\overrightarrow 0 }\) luôn bằng 1800,
– Trong trường hợp có ít nhất một trong hai vectơ \({\overrightarrow a }\) hoặc \({\overrightarrow b }\) là vectơ \({\overrightarrow 0 }\) thì ta quy ước
số đo góc giữa hai vectơ đó là tuỷ ý (từ 00 đến 1800)

Ví dụ: Cho hình vuông ABCD có tâm I là giao điểm của hai đường chéo. Tìm các góc
\(\begin{array}{l}
a)\left( {\overrightarrow {IB} ,\overrightarrow {AB} } \right)\\
b)\left( {\overrightarrow {IB} ,\overrightarrow {AI} } \right)\\
c)\left( {\overrightarrow {IB} ,\overrightarrow {DB} } \right)\\
d)\left( {\overrightarrow {IA} ,\overrightarrow {IC} } \right)
\end{array}\)
Giải
a) Ta có: \(\overrightarrow {DI} = \overrightarrow {IB} ,\overrightarrow {DC} = \overrightarrow {AB} \), suy ra \(\left( {\overrightarrow {IB} ,\overrightarrow {AB} } \right) = \left( {\overrightarrow {DI} ,\overrightarrow {DC} } \right) = \widehat {IDC} = {45^0}\)
b) Ta có: \(\overrightarrow {IC} = \overrightarrow {AI} \), suy ra \(\left( {\overrightarrow {IB} ,\overrightarrow {AI} } \right) = \left( {\overrightarrow {IB} ,\overrightarrow {IC} } \right) = \widehat {BIC} = {90^0}\)
c) Do hai vecto \(\overrightarrow {IB} ,\overrightarrow {DB} \) cùng hướng nên ta có \(\left( {\overrightarrow {IB} ,\overrightarrow {DB} } \right) = {0^0}\)
d) Do hai vecto \({\overrightarrow {IA} ,\overrightarrow {IC} }\) ngược hướng nên ta có \(\left( {\overrightarrow {IA} ,\overrightarrow {IC} } \right) = {180^0}\)
1.2. Tích vô hướng của hai vectơ
| Tích vô hướng của hai vecto \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\) |
|---|
Chú ý:
+) \(\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u \bot \;\overrightarrow v \;\;\)
+) \(\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)
Ví dụ: Cho tam giác đều ABC cỏ cạnh bằng 4 và có đường cao AH. Tính các tích vô hướng:
\(\begin{array}{l}
a){\rm{ }}\overrightarrow {AB} .\overrightarrow {AC} ;\\
b){\rm{ }}\overrightarrow {AB} .\overrightarrow {BC} ;\\
c){\rm{ }}\overrightarrow {AH} .\overrightarrow {BC}
\end{array}\)
Giải
\(\begin{array}{l}
a){\rm{ }}\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.cos\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = 4.4.cos{60^0} = 16.\frac{1}{2} = 8\\
b){\rm{ }}\overrightarrow {AB} .\overrightarrow {BC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.cos\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = 4.4.cos{120^0} = 16.\left( { – \frac{1}{2}} \right) = – 8\\
c){\rm{ }}\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.cos\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.cos{90^0} = 0
\end{array}\)
1.3. Tính chất của tích vô hướng
|
Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có: \(\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}\) |
|---|
Nhận xét
\(\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v – \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; – \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u – \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} – 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u – \overrightarrow v } \right) = {\overrightarrow u ^2} – {\overrightarrow v ^2}\end{array}\)
Ví dụ: Cho tam giác ABC. TÍnh cạnh AB theo hai cạnh còn lại và góc C
Giải
Ta có: \(A{B^2} = {\overrightarrow {AB} ^2} = {\left( {\overrightarrow {CB} – \overrightarrow {CA} } \right)^2} = {\overrightarrow {CB} ^2} + {\overrightarrow {CA} ^2} – 2\overrightarrow {CB} .\overrightarrow {CA} = {\overrightarrow {CB} ^2} + {\overrightarrow {CA} ^2} – 2CB.CA.\cos C\)
hay \({c^2} = {a^2} + {b^2} – 2.b.c.\cos C\)