Cho hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\). Từ một điểm A tùy ý, lấy hai điểm B, C sao cho  \(\overrightarrow {AB}  = \overrightarrow a \), \(\overrightarrow {BC}  = \overrightarrow b \). Khi đó \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\overrightarrow a\), \(\overrightarrow b\) được kí hiệu là \(\overrightarrow a  + \overrightarrow b \).  Vậy \(\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Quy tắc ba điểm:

Với 3 điểm M, N, P ta có: \(\overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} \)

Quy tắc hình bình hành:

Nếu OABC là hình bình hành thì ta có \(\overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB} \)

Chú ý:

+ Khi công hai vectơ theo quy tắc ba điểm, điểm cuỗi của vectơ thứ nhât phải là điểm đầu của vectơ thứ hai.

Ví dụ: Cho các điểm E, F, G, H, K. Thực hiện các phép cộng vecto

\(\overrightarrow {EF}  + \overrightarrow {FH} ;\overrightarrow {FK}  + \overrightarrow {KG} ;\overrightarrow {HF}  + \overrightarrow {HE} \)

Giải

Áp dụng quy tắc ba điểm, ta có:

\(\begin{array}{l}
\overrightarrow {EF}  + \overrightarrow {FH}  = \overrightarrow {EH} ;\\
\overrightarrow {FK}  + \overrightarrow {KG}  = \overrightarrow {FG} ;\\
\overrightarrow {HF}  + \overrightarrow {HE}  = \overrightarrow {EE}  = \overrightarrow 0.
\end{array}\)

Phép cộng vecto có các tính chất sau: + Tính chất giao hoán: \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \) + Tính chất kết hợp: \((\overrightarrow a  + \overrightarrow b ) + \overrightarrow c  = \overrightarrow a  + (\overrightarrow b  + \overrightarrow c )\) + Với mọi vecto \(\overrightarrow a ,\) ta luôn có: \(\overrightarrow a  + \overrightarrow 0  = \overrightarrow 0  + \overrightarrow a  = \overrightarrow a \)

Chú ý: \(\overrightarrow a  + ( – \overrightarrow a ) = \overrightarrow 0 \) (Tổng hai vecto đối luôn bằng vecto-không)

Ví dụ: Cho tứ giác ABCD. Thực hiện các phép cộng vecto sau: \(\left( {\overrightarrow {AB}  + \overrightarrow {CA} } \right) + \overrightarrow {BC} \)

Giải

Áp dụng tính chất giao hoán và kết hợp của phép cộng vecto, ta có:

\(\left( {\overrightarrow {AB}  + \overrightarrow {CA} } \right) + \overrightarrow {BC}  = \left( {\overrightarrow {CA}  + \overrightarrow {AB} } \right) + \overrightarrow {BC}  = \overrightarrow {CB}  + \overrightarrow {BC}  = \overrightarrow {CC}  = \overrightarrow 0 \)

Hiệu của hai vecto \(\overrightarrow a  – \overrightarrow b  = \overrightarrow a  + \left( { – \overrightarrow b } \right)\)

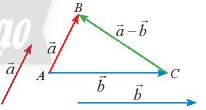
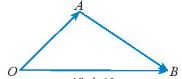
Chú ý: Cho ba điểm O, A, B ta có: \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {AB} \)

Ví dụ: Cho các điểm M, N, P, Q. Thực hiện các phép trừ vecto sau: \(\overrightarrow {MN}  – \overrightarrow {PN} ;\overrightarrow {PM}  – \overrightarrow {PQ} \)

Giải

Ta có: 

\(\begin{array}{l}
\overrightarrow {MN}  – \overrightarrow {PN}  = \overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} ;\\
\overrightarrow {PM}  – \overrightarrow {PQ}  = \overrightarrow {PM}  + \overrightarrow {QP}  = \overrightarrow {QP}  + \overrightarrow {PM}  = \overrightarrow {QM} .
\end{array}\)

+) M là trung điểm AB \( \Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 \) +) G là trọng tâm của \(\Delta ABC\) \( \Leftrightarrow \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Ví dụ: Cho tứ giác ABCD cóI, J lần lượt là trung điểm của AB, CD và O là trung điểm của IJ. Chứng minh \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0 \)

Giải

Do I, J, O lần lượt là trung điểm của AB, CD và Ị nên:

\(\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0 ;\overrightarrow {JC}  + \overrightarrow {JD}  = \overrightarrow 0 ;\overrightarrow {OI}  + \overrightarrow {OJ}  = \overrightarrow 0 \)

Ta có: 

\(\begin{array}{l}
\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \left( {\overrightarrow {OI}  + \overrightarrow {IA} } \right) + \left( {\overrightarrow {OI}  + \overrightarrow {IB} } \right) + \left( {\overrightarrow {OJ}  + \overrightarrow {JC} } \right) + \left( {\overrightarrow {OJ}  + \overrightarrow {JD} } \right)\\
 = \left( {\overrightarrow {OI}  + \overrightarrow {OJ} } \right) + \left( {\overrightarrow {IA}  + \overrightarrow {IB} } \right) + \left( {\overrightarrow {OI}  + \overrightarrow {OJ} } \right) + \left( {\overrightarrow {JC}  + \overrightarrow {JD} } \right)\\
 = \overrightarrow 0 
\end{array}\)