1.1. Định nghĩa vectơ
Đại lượng vô hướng là đại lượng chỉ có độ lớn. Ví dụ: khôi lượng, khoảng cách, nhiệt độ, …
Đại lượng có hướng là đại lượng bao gồm cả đô lớn và hướng. Ví du: đô dịch chuyền, lực, vận tốc, gia tộc,
Khi xác định một đại lượng vô hướng, ta chỉ cằn mô tả độ lớn của nó. Ví dụ: Hàng trên tàu có khôi lượng 500 tân.
Khi xác định một đại lượng có hướng, ta phải đề cập đến cả độ lớn và hướng của nó. Ví dụ: Con tàu có độ địch chuyển đài 500 km theo hướng từ A đền B.
| Vecto là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối. |
|---|
* Wectơ có điểm đầu A, điểm cuối B được kí hiệu là \(\overrightarrow {AB} \), đọc là vectơ \(\overrightarrow {AB} \) (Hình sau)
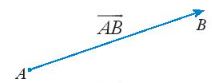
* Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ \(\overrightarrow {AB} \).
* Độ dài của đoạn thẳng AB gọi là độ đài của vectơ V và được kí hiệu là \(\left| {\overrightarrow {AB} {\rm{ }}} \right|\) Như vậy ta có: \(\left| {\overrightarrow {AB} {\rm{ }}} \right| = AB\).
Chú ý: Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là \(\overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y \)…
Ví dụ: Cho tam giác đều ABC có cạnh bằng 2 (Hình sau). Gọi H là trung điểm của đoạn thẳng BC. Tìm điểm đầu, điểm cuối, giá và độ đài của các vectơ: \(\overrightarrow {CA} ,\overrightarrow {AH} ,\overrightarrow {BH} \)
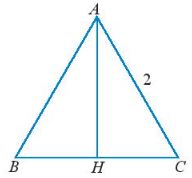
Giải
Vectơ \(\overrightarrow {CA}\) có điểm đầu là C, điểm cuôi là A và có giá là đường thẳng AC.
Veclơ \(\overrightarrow {AH}\) có điểm đầulà A, điểm cuối là H và có giá là đường thẳng AH.
Vectơ \(\overrightarrow {BH}\) có điểm đầu là B, điểm cuôi là H và có giá là đường thẳng BH.
Ta có: CA =2, BH = 1, \(AH = \sqrt {A{C^2} – C{H^2}} = \sqrt {4 – 1} = \sqrt 3 \)
Suy ra \(\left| {\overrightarrow {AC} } \right| = 2,\left| {\overrightarrow {BH} } \right| = 1,\left| {\overrightarrow {AH} } \right| = \sqrt 3 .\)
1.2. Hai vectơ cùng phương, cùng hướng
|
+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. +) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng. |
|---|
Ví dụ:
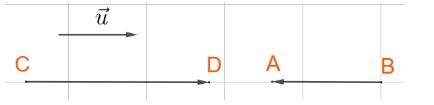
Ba vecto \(\overrightarrow u ,\;\overrightarrow {CD} ,\;\overrightarrow {AB} \) cùng phương.
Trong đó 2 vecto \(\overrightarrow u ,\;\overrightarrow {CD} \) cùng hướng, còn 2 vecto \(\overrightarrow {CD} ,\;\overrightarrow {AB} \) ngược hướng.
+) Ba điểm A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
1.3. Vectơ bằng nhau – Vectơ đối nhau
|
+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. +) Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Kí hiệu: \(\overrightarrow a = – \overrightarrow b \), (vecto \(\overrightarrow b \) là vecto đối của vecto \(\overrightarrow a \)) |
|---|
Chú ý: Với mỗi điểm O và vecto \(\overrightarrow a \) cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a \)
Ví dụ:
a) Tìm trong hình sau hai cặp vectơ bằng nhau và hai căp vectơ đối nhau.
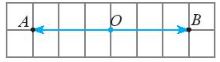
b) Cho điểm O là trung điểm của đoạn thẳng AB. Tìm hai vectơ đối nhau.
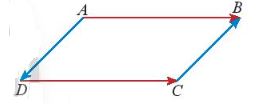
Giải
Trình hình trên, ta có:
\(\begin{array}{l}
\overrightarrow {AB} = \overrightarrow {AD} ,\overrightarrow {DA} = \overrightarrow {CB} \\
\overrightarrow {AD} = – \overrightarrow {CB} ,\overrightarrow {DA} = \overrightarrow { – AD}
\end{array}\)
b) Ta có: \(\overrightarrow {OA} = – \overrightarrow {OB} \) (Hình sau)
1.4. Vectơ không
| Vecto không, là vecto có điểm đầu và điểm cuối trùng nhau. Kí hiệu chung là \(\overrightarrow 0 \). |
|---|
Ví dụ: \(\overrightarrow {AA} ,\;\overrightarrow {EE} ,…\)
* Chú ý:
– Vecto không có độ dài bằng 0.
– Vecto \(\overrightarrow 0 \) cùng phương, cùng hướng với mọi vecto.
– Mọi vecto-không đều bằng nhau: \(\overrightarrow 0 = \overrightarrow {AA} = \;\overrightarrow {BB} = …\)
– Vecto đối của vecto-không là chính nó.