a) Toạ độ của một điểm

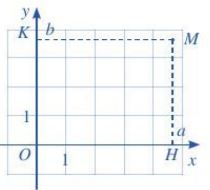
Để xác định toạ độ của một điểm M tuỳ ý trong mặt phẳng toạ độ Oxy, ta làm như sau:

+ Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

+Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm /M.

Cặp số (a; b) là toạ độ của điểm M trong mặt phẳng toạ độ Oxy. Ta kí hiệu là M(a; b).

b) Toạ độ của một vectơ

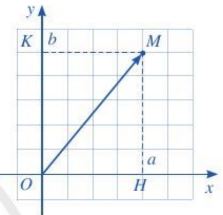
Toạ độ của điểm M được gọi là toạ độ của vectơ \(\overrightarrow {OM} \).

Nếu \(\overrightarrow {OM} \) có toạ độ (a ; b) thì ta viết \(\overrightarrow {OM} \) = (a; b), trong đó a gọi là hoành độ của vectơ \(\overrightarrow {OM} \) và b gọi là tung độ của vectơ \(\overrightarrow {OM} \) (Hình sau).

+ Với mỗi vectơ \(\overrightarrow u \) trong mặt phẳng toạ độ Oxy, toạ độ của vectơ \(\overrightarrow u \) là toạ độ của điểm A sao cho \(\overrightarrow {OA}  = \overrightarrow u \). + Trong mặt phẳng toạ độ Oxy, nếu \(\overrightarrow u  = \left( {a;b} \right)\) thì \(\overrightarrow u  = a\overrightarrow i  + b\overrightarrow j \). Ngược lại, nếu \(\overrightarrow u  = a\overrightarrow i  + b\overrightarrow j \) thì \(\overrightarrow u  = \left( {a;b} \right)\).

Chú ý: Với \(\overrightarrow a  = \left( {{x_1};{y_1}} \right)\) và \(\overrightarrow b  = \left( {{x_2};{y_2}} \right)\), ta có: \(\overrightarrow a  = \overrightarrow b  = \left\{ \begin{array}{l}
{x_1} = {x_2}\\
{y_1} = {y_2}
\end{array} \right.\)

Như vậy, mỗi vectơ hoàn toàn được xác định khi biết toạ độ của nó.

c) Liên hệ giữa toạ độ của điểm và toạ độ của vectơ

Trong mặt phẳng toạ độ Oxy, cho hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\). Ta có: \(\overrightarrow {AB}  = \left( {{x_B} – {x_A};{y_B} – {y_A}} \right)\)

a) Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto

Cho hai vectơ \(\overrightarrow a  = \left( {{a_1};{a_2}} \right),\overrightarrow b  = \left( {{b_1};{b_2}} \right)\) và số thưucj k. Khi đó:

\(\begin{array}{l}
1)\;\;\;\overrightarrow a  + \overrightarrow b  = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right);\\
2)\;\;\;\overrightarrow a  – \overrightarrow b  = \left( {{a_1} – {b_1};{a_2} – {b_2}} \right);\\
3)\;\;\;k\overrightarrow a  = \left( {k{a_1};k{a_2}} \right);\\
4)\;\;\;\overrightarrow a .\overrightarrow b  = {a_1}.{b_1} + {a_2}.{b_2}.
\end{array}\)

b) Toạ độ trung điểm đoạn thẳng và tọa độ trọng tâm của tam giác

+ Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Toa độ trung điểm \(M\left( {{x_M};{y_M}} \right)\) của đoạn thẳng AB là

\({x_M} = \frac{{{x_A} + {x_B}}}{2};{y_M} = \frac{{{y_A} + {y_B}}}{2}\)

+ Cho tam giác ABC có \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Toa độ trọng tâm \(G\left( {{x_G};{y_G}} \right)\) của tam giác ABC là:

\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\)

c) Biểu thức tọa độ của tích vô hướng

Nếu \(\overrightarrow u  = \left( {{x_1};{y_1}} \right)\) và \(\overrightarrow v  = \left( {{x_2};{y_2}} \right)\) thì \(\overrightarrow u .\overrightarrow v  = {x_1}.{x_2} + {y_1}.{y_2}\).

a) Phương trình tham số của đường thẳng

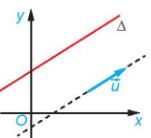
*Vectơ chỉ phương của đường thẳng

Vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) được goi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của nó song song hoặc trùng với \(\Delta \).

Nhận xét

+ Nếu \(\overrightarrow u \) là vectơ chỉ phương của đường thẳng \(\Delta \) thì k\(\overrightarrow u \) (\(k \ne 0\)) cũng là vectơ chỉ phương của \(\Delta \).

+ Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ chỉ phương của nó.

+ Hai vectơ \(\overrightarrow n \left( {a;b} \right)\) và \(\overrightarrow u \left( {-b;a} \right)\) vuông góc với nhau nên nêu \(\overrightarrow n \) là vectơ pháp tuyến của đường thẳng \(\Delta \) thì \(\overrightarrow u \) là vectơ chỉ phương của đường thẳng đó và ngược lại.

*Phương trình tham số của đường thẳng

Cho đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u \left( {a;b} \right)\). Khi đó điểm M(x: y) thuộc đường thẳng \(\Delta \) khi và chỉ khi tổn tại số thực t sao cho \(\overrightarrow {AM}  = t\overrightarrow u \), hay \(\left\{ \begin{array}{l} x = {x_0} + at\\ y = {y_0} + bt \end{array} \right.\;\;\;\;\;\;\;\;(2)\) Hệ (2) được gọi là phương trình tham số của đường thẳng \(\Delta \) (t là tham số).

b) Phương trình tổng quát của đường thẳng

*Vectơ pháp tuyến của đường thẳng

Vectơ \(\overrightarrow n \) khác \(\overrightarrow 0 \)được gọi là vectơ pháp tuyến của đường thẳng \(\Delta \) nếu giá của nó vuông góc với \(\Delta \).

Nhận xét

+ Nếu \(\overrightarrow n \) là vectơ pháp tuyến của đường thẳng \(\Delta \) thi k\(\overrightarrow n \) (\(k \ne 0\)) cũng là vectơ pháp tuyến của \(\Delta \).

+ Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ pháp tuyến của nó.

*Phương trình tổng quát của đường thẳng

Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng ax + by + c =0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax + by + c =0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.

Nhận xét: Trong mặt phẳng toạ độ, cho đường thẳng \(\Delta \): ax + by + c = 0

+ Nếu b = 0 thì phương trình \(\Delta \) có thể đưa về dạng x = m (với \(m =  – \frac{c}{a}\)) và \(\Delta \) vuông góc với Ox.

+ Nếu \(b \ne 0\) thì phương trình \(\Delta \) có thể đưa về dạng y =  nx + p (với \(n =  – \frac{a}{b},p =  – \frac{c}{b}\))

c) Lập phương trình đường thẳng

Khi lập phương trình đường thẳng, ta thường gặp ba trường hợp như sau:

– Lập phương trình đường thẳng đi qua một điểm cho trước và biết vectơ pháp tuyến.

– Lập phương trình đường thẳng đi qua một điểm cho trước và biết vectơ chỉ phương.

– Lập phương trình đường thẳng đi qua hai điểm cho trước.

*Lập phương trình đường thẳng đi qua một điểm và biết vectơ pháp tuyến

Phương trình đường thẳng \(\Delta\) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n  = \left( {a;b} \right)\left( {\overrightarrow n  \ne \overrightarrow 0 } \right)\) làm vectơ pháp tuyến là \(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0\).

*Lập phương trình đường thẳng đi qua một điểm và biết vectơ chỉ phương

Phương trình tham số của đường thẳng \(\Delta\) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow u  = \left( {a;b} \right)\left( {\overrightarrow u  \ne \vec 0} \right)\) làm vectơ chỉ phương là \(\left\{ \begin{array}{l}
x = {x_0} + at\\
y = {y_0} + bt
\end{array} \right.\) (t là tham số).

Nếu \(a \ne 0\) và \(b \ne 0\) thì ta còn có thể viết phương trình của đường thẳng A ở dạng: \(\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b}\). 

*Lập phương trình đường thẳng đi qua hai điểm

Đường thẳng \(\Delta\) đi qua hai điểm \(A\left( {{x_0};{y_0}} \right),B\left( {{x_1};{y_1}} \right)\) nên nhận vectơ \(\overrightarrow {AB}  = \left( {{x_1} – {x_0};{y_1} – {y_0}} \right)\) làm vectơ chỉ phương. Do đó. phương trình tham số của đường thẳng \(\Delta\) là:

\(\left\{ \begin{array}{l}
x = {x_0} + \left( {{x_1} – {x_0}} \right)t\\
y = {y_0} + \left( {{y_1} – {y_0}} \right)t
\end{array} \right.\) (t là tham số).

Nếu \({x_1} – {x_0} \ne 0\) và \({y_1} – {y_0} \ne 0\) thì ta còn có thể viết phương trình của đường thẳng \(\Delta\) ở dạng:

\(\frac{{x – {x_0}}}{{{x_1} – {x_0}}} = \frac{{y – {y_0}}}{{{y_1} – {y_0}}}\)

a) Vị trí tương đối của hai đường thẳng

Trong mặt phẳng tọa độ, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượtcó các vectơ chỉ phương \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) ta có: 

+ \({\Delta _1}\) cắt \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) không cùng phương.

+ \({\Delta _1}\) song song \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.

+ \({\Delta _1}\) trùng với \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương và có một điểm thuộc cả hai đường thẳng đó. 

b) Góc giữa hai đường thẳng

– Hai đường thẳng cắt nhau tạo thành bốn góc, số đo của góc không tù được gọi là số đo góc (hay đơn giản là góc) giữa hai đường thẳng.

– Góc giữa hai đường thẳng song song hoặc trùng nhau được quy ước bằng 0°.

– Cho hai đường thẳng

\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\).

Với các vectơ pháp tuyến \(\overrightarrow {{n_1}} \left( {{a_1};{b_1}} \right)\) và \(\overrightarrow {{n_2}} \left( {{a_2};{b_2}} \right)\) trong ứng. Khi đó, góc \(\varphi \) giữa hai đường thằng đó được xác định thông qua công thức

\(cos\varphi  = \left| {cos\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} .\sqrt {{a_2}^2 + {b_2}^2} }}\)

Chú ý

+ \({\Delta _1} \bot {\Delta _2} \Leftrightarrow \overrightarrow {{n_1}}  \bot \overrightarrow {{n_2}}  \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} = 0\). 

+ Nếu \({\Delta _1},{\Delta _2}\) có các vectơ chỉ phương \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) thì góc \(\varphi \) giữa \({{\Delta _1}}\) Và \({{\Delta _2}}\) cũng được xác định thông qua công thứ \(cos\varphi  = \left| {cos\left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right|\) 

c) Khoảng cách từ một điểm đến một đường thẳng

Cho điểm \(M\left( {{x_0};{y_0}} \right)\) và đường thẳng \(\Delta :ax + by + c = 0\). Khoảng cách từ điểm M đến đường thẳng \(\Delta \), kí hiệu là \(d\left( {M,\Delta } \right)\), được tính bởi công thức

\(d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

a) Phương trình đường tròn

Phương trình đường tròn tâm I(a; b) bán kính R là  \({\left( {x – a} \right)^2} + {\left( {y – b} \right)^2} = {R^2}\).

Phương trình đường tròn ở dạng trên thường được gọi là phương trình chính tắc của đường tròn.

b) Phương trình tiếp tuyến của đường tròn

Phương trình tiếp tuyến của đường tròn tâm I(a, b) tại điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn là: \(\left( {a – {x_0}} \right)\left( {x – {x_0}} \right) + \left( {b – {y_0}} \right)\left( {y – {y_0}} \right) = 0\)

a) Đường Elip

+ Trong mặt phẳng toạ độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điềm của đoạn nối hai tiêu điểm đó, thì có phương trình

\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\).             (1)

+ Ngược lại, mỗi phương trình có dạng (1), với a > b > 0, đều là phương trình của elip có hai tiêu điểm \({F_1}\left( { – \sqrt {{a^2} – {b^2}} ;0} \right),{F_2}\left( {\sqrt {{a^2} – {b^2}} ;0} \right)\), tiêu cự \(2c = 2\sqrt {{a^2} – {b^2}} \) và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a.

Phương trinh (1) được gọi là phương trình chính tắc của elip tương ứng.

b) Đường Hypebol

+ Cho hai điểm phân biệt có định \({F_1}\) và \({F_2}\). Đặt \({F_1}{F_2} = 2c\). Cho số thực dương a nhỏ hơn c. Tập hợp các điểm M sao cho \(\left| {M{F_1} – M{F_2}} \right| = 2c\) được gọi là đường hypebol (hay hypebol). Hai điểm \({{F_1},{F_2}}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của hypebol đó.

+ Trong mặt phẳng toạ độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó, thì có phương trình

\(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a,b > 0\).      (2)

+ Ngược lại, mỗi phương trình có dạng (2), với a, b >0, đều là phương trình của hypebol có hai tiêu điểm \({F_1}\left( { – \sqrt {{a^2} + {b^2}} ;0} \right),{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right)\), tiêu cự \(2c = 2\sqrt {{a^2} + {b^2}} \) và giá trị tuyệt đối của hiệu các khoảng cách từ mối điểm thuộc hypebol đến hai tiêu điểm bằng 2a.

Phương trình (2) được gọi là phương trình chính tắc của hypebol tương ứng.

c) Đường Parabol

+ Cho một điểm F có định và một đường thẳng \(\Delta \) cố định không đi qua F. Tập hợp các điểm M cách đều F và \(\Delta \) được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, \(\Delta \) được gọi là đường chuẩn, khoảng cách từ F đến \(\Delta \) được gọi là tham số tiêu của parabol đó. 

+ Xét (P) là một parabol với tiêu điểm F, đường chuẩn \(\Delta \). Gọi H là hình chiếu vuông góc của F trên \(\Delta \). Khi đó, trong hệ trục toạ độ Oxy với gốc O là trung điểm của HF, tia Ox trùng tia OF, parabol (P) có phương trình

\({y^2} = 2p{\rm{x}}\) (với p > 0)        (3)

Phương trình (3) được gọi là phương trình chính tắc của parabol (P).

+ Ngược lại, mỗi phương trình dạng (3), với p > 0, là phương trình chính tắc của parabol có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\) và đường chuẩn \(\Delta 😡 =  – \frac{p}{2}\).

d) Một số ứng dụng thực tiễn của ba đường conic

– Ba đường conic có nhiều ứng dụng trong thực tiễn. Ta nêu ra một vài ứng dụng của ba đường conic.

+ Năm 1911, nhà vật lí học người Anh là Ernest Rutherford (1871 – 1937) đã để xuất mô hình hành tỉnh nguyên tử, trong đó hạt nhân nhỏ bé nằm tại tâm của nguyên tử, còn các electron bay quanh hạt nhân trên các quỹ đạo hình elip như các hành tỉnh bay quanh Mặt Trời (Hình sau).

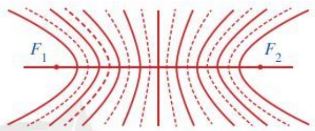
+ Trong vật lí, hiện tượng hai sóng gặp nhau tạo nên các gợn sóng ổn định gọi là hiện tượng giao thoa của hai sóng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa (Hình sau).

+ Với gương parabol, tia sáng phát ra từ tiêu điểm (tia tới) chiếu đến một điểm của parabol sẽ bị hắt lại (ủa phản xạ) theo một tỉa song song (hoặc trùng) với trục của parabol (Hình sau).

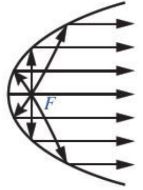
– Tính chất trên có nhiều ứng dụng, chẳng hạn:

+ Đèn pha: Bề mặt của đèn pha là một mặt tròn xoay sinh bởi một cung parabol quay quanh trục của nó, bóng đèn được đặt ở vị trí tiêu điểm của parabol đó (Hình sau). Các tia sáng phát ra từ bóng đèn khi chiếu đến bề mặt của đèn pha sẽ bị hắt lại theo các tỉa sáng song song, cho phép chúng ta quan sát được các vật ở xa.

+ Chảo vệ tỉnh cũng có dạng như đèn pha. Điểm thu và phát tín hiệu của máy được đặt ở vị trí tiêu điểm của parabol (Hình sau).