a) Giá trị lượng giác của một góc từ \({0^0}\) đến \({180^0}\)

+) Với mỗi góc \(\alpha ({0^o} \le \alpha {\rm{\;}} \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\) Khi đó: \(\sin \alpha {\rm{\;}} = {y_0}\) là tung độ của M \(\cos \alpha {\rm{\;}} = {x_0}\) là hoành độ của M \(\tan \alpha {\rm{\;}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha {\rm{\;}} \ne {90^o})\) \(\cot \alpha {\rm{\;}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha {\rm{\;}} \ne {0^o},\alpha {\rm{\;}} \ne {180^o})\)

*Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Hai góc bù nhau, \(\alpha \) và \({180^o} – \alpha \):

\(\begin{array}{*{20}{l}}{\sin \left( {{{180}^o} – \alpha } \right) = \sin \alpha }\\{\cos \left( {{{180}^o} – \alpha } \right) = {\rm{\;}} – \cos \alpha }\\{\tan \left( {{{180}^o} – \alpha } \right) = {\rm{\;}} – \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o})}\\{\cot \left( {{{180}^o} – \alpha } \right) = {\rm{\;}} – \cot \alpha ({0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}\) 

Hai góc phụ nhau, \(\alpha \) và \({90^o} – \alpha \):

\(\begin{array}{*{20}{l}}{\sin \left( {{{90}^o} – \alpha } \right) = \cos \alpha }\\{\cos \left( {{{90}^o} – \alpha } \right) = \sin \alpha }\\{\tan \left( {{{90}^o} – \alpha } \right) = \cot \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\\{\cot \left( {{{90}^o} – \alpha } \right) = \tan \alpha (\alpha {\rm{\;}} \ne {{90}^o},{0^o} < \alpha {\rm{\;}} < {{180}^o})}\end{array}\) 

*Các giá trị lượng giác của một số góc đặc biệt

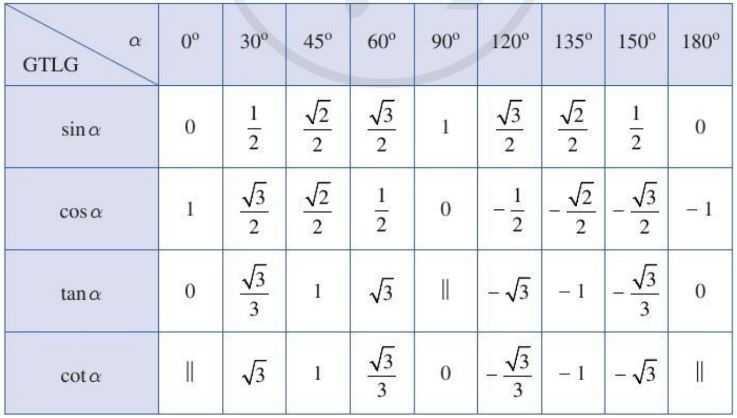
b) Định lí Côsin

Trong tam giác ABC: \(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} – 2bc\cos A}\\{{b^2} = {c^2} + {a^2} – 2ca\cos B}\\{{c^2} = {a^2} + {b^2} – 2ab\cos C}\end{array}\)

* Hệ quả

\(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}\)

c) Định lí Sin

Trong tam giác ABC: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\) (R là bán kính đường tròn ngoại tiếp tam giác ABC)

* Hệ quả

\(a = 2R.\sin A;\quad b = 2R\sin B;\quad c = 2R\sin C\)

\(\sin A = \frac{a}{{2R}};\quad \sin B = \frac{b}{{2R}};\quad \sin C = \frac{c}{{2R}}.\)

a) Tính các cạnh và góc của tam giác dựa trên một số điều kiện cho trước

Một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:

– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó:

– Biết độ dài ba cạnh;

– Biết độ dài một cạnh và độ lớn hai góc kể với cạnh đó.

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

b) Tính diện tích tam giác

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}ca.\sin B = \frac{1}{2}ab.\sin C.\)

Ta có công thức Heron để tính diện tích tam giác theo độ dài ba cạnh của nó như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, \(p = \frac{{a + b + c}}{2}\). Khi đó, diện tích S của tam giác ABC là:

\(S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \)

a) Khái niệm

Vectơ là một đoạn thẳng có hướng

– Vectơ có điểm đầu là A, điểm cuối là B được kí hiệu là \(\overrightarrow {AB} \), đọc là ““vectơ AB”.

– Để vẽ vectơ \(\overrightarrow {AB} \) ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu mút B (hình sau).

Đối với vectơ \(\overrightarrow {AB} \), ta gọi:

+ Đường thẳng d đi qua hai điểm A và B là giá của vectơ \(\overrightarrow {AB} \) (hình sau):

+ Độ dài đoạn thẳng AB là độ dài của vectơ \(\overrightarrow {AB} \), kí hiệu là \(\left| {\overrightarrow {AB} } \right|\).

b) Vectơ cùng phương, vectơ cùng hướng

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. 

Nhận xét: Nếu hai vectơ cùng phương thì hoặc chúng cùng hướng hoặc chúng ngược hướng.

c) Hai vectơ bằng nhau

Hai vectơ \({\overrightarrow {AB} }\) bằng nhau nêu chúng cùng hướng và cùng độ dài, kí hiệu: \(\overrightarrow {AB}  = \overrightarrow {C{\rm{D}}} \)

Khi không cẩn chỉ rõ điểm đậu và điểm cuối của vectơ, vectơ còn được kí hiệu là \(\overrightarrow a ,\overrightarrow b ,\overrightarrow u ,\overrightarrow v \),… (Hình sau). Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\). 

Nhận xét

* Hai vectơ \(\overrightarrow a ,\overrightarrow b\) bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu \(\overrightarrow a = \overrightarrow b\).

* Khi cho trước vectơ \(\overrightarrow a\) và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho \(\overrightarrow {OA}  = \overrightarrow a \).

d) Vectơ không

Vectơ- không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là \(\overrightarrow 0 \).

Với các điểm bất kì A, B, C ta có: \(\overrightarrow 0  = \overrightarrow {AA}  = \overrightarrow {BB}  = \overrightarrow {CC} \). 

Vectơ \(\overrightarrow {AA} \) nằm trên mọi đường thẳng đi qua A. Ta quy ước \(\overrightarrow 0\) (vectơ-không) cùng phương và cùng hướng với mọi vectơ; \(\left| {\overrightarrow 0 } \right| = \overrightarrow 0 \). 

Nhận xét: Hai điểm A, trùng nhau khi và chỉ khi \(\overrightarrow {AB}  = \overrightarrow 0 \).

a) Tổng của hai vectơ

Cho hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\). Từ một điểm A tùy ý, lấy hai điểm B, C sao cho  \(\overrightarrow {AB}  = \overrightarrow a \), \(\overrightarrow {BC}  = \overrightarrow b \). Khi đó \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\overrightarrow a\), \(\overrightarrow b\) được kí hiệu là \(\overrightarrow a  + \overrightarrow b \).  Vậy \(\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Quy tắc ba điểm:

Với 3 điểm M, N, P ta có: \(\overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} \)

Quy tắc hình bình hành:

Nếu OABC là hình bình hành thì ta có \(\overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB} \)

– Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tuỳ ý:

• Tính chất giao hoán: \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \)
• Tính chất kết hợp: \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\)
• Tính chất của vectơ-không: \(\overrightarrow a  + \overrightarrow 0  = \overrightarrow 0  + \overrightarrow a  = \overrightarrow a \)  

b) Hiệu của hai vectơ

– Vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \) – Vectơ đối của \(\overrightarrow a \) được kí hiệu là \(-\overrightarrow a \). – Vectơ \(\overrightarrow 0 \) được coi là vectơ đối của chính nó. – Vectơ \(\overrightarrow a  + \left( { – \overrightarrow b } \right)\) được gọi là hiệu của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a  – \overrightarrow b \). Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

Chú ý: 

– Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng \(\overrightarrow 0 \).

– Nếu \(\overrightarrow b  + \overrightarrow c  = \overrightarrow a \) thì \(\overrightarrow a  – \overrightarrow b  = \overrightarrow a  + \left( { – \overrightarrow b } \right) = \overrightarrow c  + \overrightarrow b  + \left( { – \overrightarrow b } \right) = \overrightarrow c  + \overrightarrow 0  = \overrightarrow c \)

– Với ba điểm O, M, N tuỷ ý, ta có \(\overrightarrow {MN}  = \overrightarrow {MO}  + \overrightarrow {ON}  = \left( { – \overrightarrow {OM} } \right) + \overrightarrow {ON}  = \overrightarrow {ON}  – \overrightarrow {OM} \)

– Quy tắc hiệu: Với ba điểm O, M, N, ta có \(\overrightarrow {MN}  = \overrightarrow {ON}  – \overrightarrow {OM} \)

a) Định nghĩa

+) Tích của một số thực \(k\) với một vecto \(\overrightarrow a  \ne \overrightarrow 0 \) là một vecto, kí kiệu là \(k\overrightarrow a .\) +) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và cùng hướng với vecto \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vecto \(\overrightarrow a \) nếu \(k < 0\)

Quy ước: \(0\;\overrightarrow a  = \overrightarrow 0 \) và \(k\;\overrightarrow 0  = \overrightarrow 0 \)

b) Tính chất

Với hai vecto \(\overrightarrow a ,\overrightarrow b \) và hai số thực \(k,t\) ta luôn có:

\(\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a  = k\overrightarrow a  + t\overrightarrow a \\k(\overrightarrow a  + \overrightarrow b ) = k\overrightarrow a  + k\overrightarrow b ;\quad k(\overrightarrow a  – \overrightarrow b ) = k\overrightarrow a  – k\overrightarrow b \\1\;\overrightarrow a  = \overrightarrow a ;\;\;( – 1)\;\overrightarrow a  =  – \,\overrightarrow a \end{array}\)

c) Một số ứng dụng

– Nếu I là trung điểm của đoạn thẳng AB thì \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \) với điểm M bất kì.

– Nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 2\overrightarrow {MG} \) với điểm M bất kì.

* Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng.

– Điều kiện cần và đủ để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) (\(\overrightarrow b  \ne \overrightarrow 0 \)) cùng phương là có một số thực k để \(\overrightarrow a  = k\overrightarrow b \). 

– Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để \(\overrightarrow {AB}  = k\overrightarrow {AC} \). 

a) Định nghĩa

Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) khác \({\vec 0}\). Từ một điểm A tuỳ ý, vẽ các vectơ \(\overrightarrow {AB}  = \overrightarrow u \) và \(\overrightarrow {AC}  = \overrightarrow v \) (Hình cho bên dưới). Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay đơn giản là góc giữa hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) kí hiệu là \(\left( {\overrightarrow u ,\overrightarrow v } \right)\).

Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u .\overrightarrow v \), được xác định bởi công thức sau: \(\overrightarrow u .\overrightarrow v  = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.cos\left( {\overrightarrow u ,\overrightarrow v } \right)\)

Chú ý: 

+ Quy ước rằng góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow 0 \) có thể nhận một giá trị tuỳ ý từ 0° đến 180°.

+ Nếu \(\left( {\overrightarrow u ,\overrightarrow v } \right) = {90^0}\) thì ta nói rằng \(\overrightarrow u \) và \(\overrightarrow v \) vuông góc với nhau, kí hiệu là \({\overrightarrow u  \bot \overrightarrow v }\) hoặc \({\overrightarrow v  \bot \overrightarrow u }\). Đặc biệt \(\overrightarrow 0 \) được coi là vuông góc với mọi vectơ.

\(\overrightarrow u  \bot \overrightarrow v  \Leftrightarrow \overrightarrow u .\overrightarrow v  = \overrightarrow 0 \)

\(\overrightarrow u .\overrightarrow u \) còn được viết là \({\overrightarrow u ^2}\). Ta có \({\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.cos{0^0} = {\left| {\overrightarrow u } \right|^2}\) 

b) Tính chất

Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có: \(\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v  + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v  = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}\)

Nhận xét

\(\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v  – \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; – \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u  + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u  – \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} – 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u  + \overrightarrow v } \right)\left( {\overrightarrow u  – \overrightarrow v } \right) = {\overrightarrow u ^2} – {\overrightarrow v ^2}\end{array}\)

c) Một số ứng dụng

* Tính độ dài của đoạn thẳng

– Với hai điểm A, 8 phân biệt, ta có: \({\overrightarrow {AB} ^2} = {\left| {\overrightarrow {AB} } \right|^2}\).

– Do đó độ dài đoạn thẳng AB được tính như sau: \(\overrightarrow {AB}  = \sqrt {{{\overrightarrow {AB} }^2}} \). 

* Chứng mỉnh hai đường thẳng vuông góc

– Cho hai vectơ bất kì \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Ta có: \(\overrightarrow a .\overrightarrow b  = 0 \Leftrightarrow \overrightarrow a  \bot \overrightarrow b .\)

– Hai đường thẳng AB và CD vuông góc với nhau khi và chỉ khi \(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}}  = 0\).

– Cũng như vậy, hai đường đường thẳng a và b vuông góc khi và chỉ khi \(\overrightarrow u .\overrightarrow v  = 0\), trong đó \(\overrightarrow u  \ne \overrightarrow 0 ,\overrightarrow v  \ne \overrightarrow 0 \), giá của vectơ \(\overrightarrow u \) song song hoặc trùng với đường thẳng a và giá của vectơ \(\overrightarrow v \) song song hoặc trùng với đường thẳng b.