1.1. Khái niệm vectơ
Vectơ là một đoạn thẳng có hướng
– Vectơ có điểm đầu là A, điểm cuối là B được kí hiệu là \(\overrightarrow {AB} \), đọc là ““vectơ AB”.
– Để vẽ vectơ \(\overrightarrow {AB} \) ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu mút B (hình sau).

Đối với vectơ \(\overrightarrow {AB} \), ta gọi:
+ Đường thẳng d đi qua hai điểm A và B là giá của vectơ \(\overrightarrow {AB} \) (hình sau):

+ Độ dài đoạn thẳng AB là độ dài của vectơ \(\overrightarrow {AB} \), kí hiệu là \(\left| {\overrightarrow {AB} } \right|\).
Ví dụ: Tính độ dài của các vectơ \(\overrightarrow {AB} ,\overrightarrow {C{\rm{D}}} \) và \(\overrightarrow {MN} \) ở hình sau, biết rằng độ dài cạnh của ô vuông bằng 1cm.
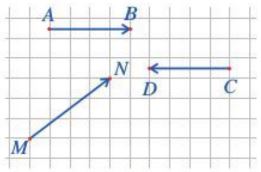
Giải
\(\begin{array}{l}
\left| {\overrightarrow {AB} } \right| = 4cm,\left| {\overrightarrow {C{\rm{D}}} } \right| = 4cm,\\
\left| {\overrightarrow {MN} } \right| = \sqrt {{3^2} + {4^2}} = 5\left( {cm} \right).
\end{array}\)
1.2. Vectơ cùng phương, vectơ cùng hướng
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Nhận xét: Nếu hai vectơ cùng phương thì hoặc chúng cùng hướng hoặc chúng ngược hướng.
Ví dụ: Trong hình sau, tìm vectơ cùng hướng với vectơ \({\overrightarrow {AB} }\); ngược hướng với vectơ \({\overrightarrow {AB} }\).
Giải
Vectơ \({\overrightarrow {CD} }\) cùng hướng với \({\overrightarrow {AB} }\), vectơ \({\overrightarrow {MN} }\) ngược hướng với vectơ \({\overrightarrow {AB} }\).
1.3. Hai vectơ bằng nhau
|
Hai vectơ \({\overrightarrow {AB} }\) bằng nhau nêu chúng cùng hướng và cùng độ dài, kí hiệu: \(\overrightarrow {AB} = \overrightarrow {C{\rm{D}}} \) |
|---|
Khi không cẩn chỉ rõ điểm đậu và điểm cuối của vectơ, vectơ còn được kí hiệu là \(\overrightarrow a ,\overrightarrow b ,\overrightarrow u ,\overrightarrow v \),… (Hình sau). Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
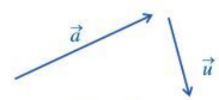
Nhận xét
* Hai vectơ \(\overrightarrow a ,\overrightarrow b\) bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu \(\overrightarrow a = \overrightarrow b\).
* Khi cho trước vectơ \(\overrightarrow a\) và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho \(\overrightarrow {OA} = \overrightarrow a \).
Ví dụ: Cho hình bình hành ABCD (Hình sau).
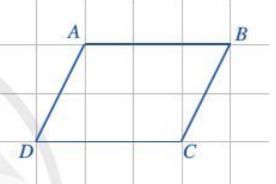
a) Vectơ nào bằng vectơ \(\overrightarrow {AB} \)?
b) Vectơ nào bằng vectơ \(\overrightarrow {AD} \).
Giải
a) Vì \(\overrightarrow {AB} ,\overrightarrow {DC} \) cùng hướng và AB = DC nên \(\overrightarrow {AB} = \overrightarrow {DC} \).
b) Vì \(\overrightarrow {AD} ,\overrightarrow {BC} \) cùng hướng và AD = BC nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
1.4. Vectơ không
|
Vectơ- không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là \(\overrightarrow 0 \). |
|---|
Với các điểm bất kì A, B, C ta có: \(\overrightarrow 0 = \overrightarrow {AA} = \overrightarrow {BB} = \overrightarrow {CC} \).
Vectơ \(\overrightarrow {AA} \) nằm trên mọi đường thẳng đi qua A. Ta quy ước \(\overrightarrow 0\) (vectơ-không) cùng phương và cùng hướng với mọi vectơ; \(\left| {\overrightarrow 0 } \right| = \overrightarrow 0 \).
Nhận xét: Hai điểm A, trùng nhau khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow 0 \).
1.5. Biểu thị một số đại lượng có hướng bằng vectơ
Trong vật lí, một số đại lượng như: lực, vận tốc, … là đại lượng có hướng. Người ta dùng vectơ để biểu thị các đại lượng có hướng đó, chẳng hạn:
Một lực \(\overrightarrow F\) tác động lên xe tại điểm đặt A; lực \(\overrightarrow F\) có phương nằm ngang, hướng từ sang phải và cường, độ là 40 N. Ta biểu thị lực \(\overrightarrow F\) bằng vectơ \(\overrightarrow AB\) như hình sau.
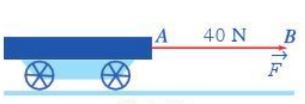
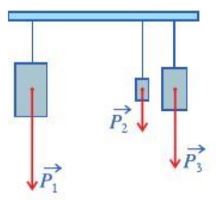
Ví dụ: Khi treo ba vật, mỗi vật sẽ tác dụng vào thanh treo một lực (trọng lực) như ở Hình sau. Nhận xét đặc điểm về phương, hướng của ba vectơ biểu thị trọng lực.
Giải
Trong vật lí, các vectơ trọng lực có cùng hướng nên ba vectơ \(\overrightarrow {{P_1}} ,\overrightarrow {{P_2}} ,\overrightarrow {{P_3}} \) biểu thị trọng lực có cùng hướng.