– Trong cuộc sống hằng ngày ta gặp nhiều vật chuyển động tròn như: bánh xe ô tô,bánh xe đạp, kim đồng hồ, đu quay,…

– Để xác định vị trí của vật chuyển động tròn ta có thể dựa vào quãng đường đi s (độ dài cung tròn) hoặc độ dịch chuyển góc \(\theta \) tính từ vị trí ban đầu.

– Khi vật chuyển động tròn trong thời giant từ A đến B thì độ dịch chuyển góc của vật trong thời gian này là góc ở tâm \(\theta \) chắn cung AB có độ dài s bằng quãng đường đi được cũng trong thời gian đó (Hình 31.1).

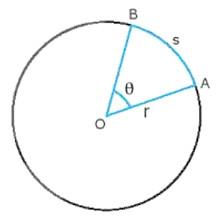
Hình 31.1. Quãng đường s và độ dịch chuyển góc \(\theta \)

– Trong Toán học, ta đã biết mối quan hệ giữa độ dài cùng với góc chắn tâm và bán kính đường tròn: \(\theta  = \frac{s}{r}\)    (31.1)

– Trong Vật lí người ta thường đo góc theo đơn vị radian (kí hiệu rad). Có thể dễ dàng chuyển đổi vị độ sang rad. Ví dụ, khi vật chuyển động được 1 vòng tròn, ta có:

\(\theta  = \frac{{2.\pi .r}}{r} = 2.\pi \)

– Do đó: 360° = \(2.\pi \) rad

– Tương tự, ta có: 180° = \(2.\pi \) rad.

– Chuyển động của một vật theo quỹ đạo tròn với tốc độ không đổi gọi là chuyển động tròn đều. – Một radian là góc ở tâm chắn cung có độ dài bằng bán kính đường tròn.

a. Tốc độ

– Trong chuyển động tròn, để đặc trưng cho sự nhanh hay chậm ta cũng dùng khái niệm tốc độ như trong chuyển động thẳng.

– Chuyển động tròn đều là chuyển động theo quỹ đạo tròn có tốc độ không thay đổi:

\(v = \frac{s}{t}\) = hằng số           (31.2)

b. Tốc độ góc

– Tốc độ góc trong chuyển động tròn đều bằng độ dịch chuyển góc chia cho thời gian dịch chuyển.

\(\omega  = \frac{\theta }{t}\)     (31.3)

– Đơn vị thường dùng của tốc độ góc là rad/s.

– Từ công thức (31.1) và (31.2), suy ra: \(v = \omega .r\)    (31.4)

với \(\omega \) là tốc độ góc có đơn vị là (rad/s).

– Tốc độ, tốc độ góc và bán kính quỹ đạo liên hệ với nhau theo công thức: \(v = \omega .r\)

– Ta đã biết trong chuyển động thẳng vận tốc tức thời \(\overrightarrow v \) tại một thời điểm cho bởi:

\(\overrightarrow v  = \frac{{\Delta \overrightarrow d }}{{\Delta t}}\)

– Khi \({\Delta t}\) rất nhỏ, vectơ độ dịch chuyển \({\Delta \overrightarrow d }\) sẽ tiến tới trùng với tiếp tuyến với đường tròn. Do đó, tại mỗi thời điểm vectơ vận tốc tức thời sẽ có phương trùng với tiếp tuyến của đường tròn (Hình 31.2).

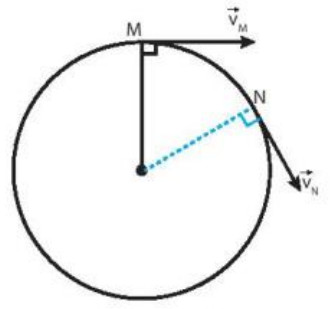
Hình 31.2. Vectơ vận tốc trong chuyển động tròn

– Trong chuyển động tròn đều, độ lớn của vận tốc tức thời không đổi nhung hướng luôn thay đổi.

Trong chuyển động tròn đều, độ lớn vận tốc không đổi những hướng luôn thay đổi.