– Tổng hợp lực là phép thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt như các lực ấy.

– Lực thay thế này gọi là hợp lực.

– Về mặt toán học, ta có thể tìm hợp lực bằng phép cộng vectơ:

\(\overrightarrow {{F}} \) = \(\overrightarrow {{F_1}} \) + \(\overrightarrow {{F_2}} \) + \(\overrightarrow {{F_3}} \) + … (13.1) 

a. Tổng hợp hai lực cùng phương

– Vật chịu tác dụng của hai lực cùng phương, cùng chiều nên lực tổng hợp cũng cùng phương, cùng chiều với hai lực thành phần và có độ lớn bằng tổng của hai lực thành phần cộng lại: \(F = {F_1} + {F_2}\)

– Vật chịu tác dụng của hai lực cùng phương, ngược chiều nên lực tổng hợp sẽ có chiều giống với lực thành phần có độ lớn lớn hơn. Độ lớn: \(F = \left| {{F_1} – {F_2}} \right|\)

b. Tổng hợp hai lực đồng quy – Quy tắc hình bình hành

– Từ các thí nghiệm và thực tế, người ta thấy rằng phép tổng hợp hai lực đồng quy tuân theo quy tắc hình bình hành sau đây (Hình 13.3):

+ Bước 1: Vẽ hai vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đồng quy tại 0.

+ Bước 2: Vẽ một hình bình hành có hai cạnh liền kề trùng với hai vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).

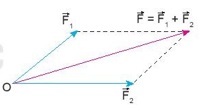
Hình 13.3. Tổng hợp lực theo quy tắc hình bình hành

+ Bước 3: Vẽ đường chéo hình bình hành có cùng gốc 0. Vectơ hợp lực \(\overrightarrow {{F_1}} \) trùng với đường chéo này.

– Tổng hợp lực là phép thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt như các lực ấy. Lực thay thế này gọi là hợp lực. – Tổng hợp hai lực cùng phương và đồng quy đều tuân theo quy tắc cộng véc tơ.

a. Các lực cân bằng

– Xét trường hợp vật đứng bên dưới tác dụng của nhiều lực. Khi đó tổng hợp các lực tác dụng lên vật bằng 0. Ta nói các lực tác dụng lên vật là các lực cân bằng và vật ở trạng thái cân bằng.

\(\overrightarrow {{F}} \) = \(\overrightarrow {{F_1}} \) + \(\overrightarrow {{F_2}} \) + \(\overrightarrow {{F_3}} \) + … = 0   (13.2)

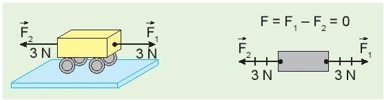
Hình 13.4. Hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cân bằng nhau

b. Các lực không cân bằng

– Khi hợp lực của các lực khác 0 thì các lực này không cân bằng. Hợp lực hay lực không cần bằng này tác dụng vào một vật có thể làm thay đổi vận tốc của vật. 

– Nếu các lực tác dụng lên một vật cân bằng nhau thì hợp lực tác dụng lên vật bằng 0. – Nếu các lực tác dụng lên một vật không cân bằng thì hợp lực tác dụng lên vật đó khác 0. Khi đó, vận tốc của vật thay đổi (độ lớn, hướng).

Phân tích lực là phép thay thế một lực thành hai lực thành phần có tác dụng giống hệt như lực ấy.

a. Quy tắc

– Thường người ta phân tích lực thành hai lực vuông góc với nhau để lực thành phần này không có tác dụng nào theo phương của lực thành phần kia.

– Phân tích lực là phép làm ngược lại với tổng hợp lực nhưng chỉ được áp dụng vào trường hợp riêng nêu ở trên. Hình 13.8 cho biết cách phân tích một lực \(\overrightarrow {{F}} \) theo hai trục.

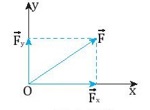
Hình 13.8

b. Chú ý

– Chỉ khi xác định được một lực có tác dụng theo hai phương vuông góc góc nào thì mới phân tích lực theo hai phương vuông góc đó.

c. Ví dụ

– Xét một vật đang trượt trên một mặt phẳng nghiêng nhẵn (Hình 13.9). Trọng lực \(\overrightarrow {{P}} \) có tác dụng: một mặt nó ép vật vào mặt phẳng nghiêng, mặt khác nó kéo vật trượt theo mặt phẳng nghiêng xuống dưới.

– Vì thế ta phân tích trong lực \(\overrightarrow {{P}} \) theo hai phương vuông góc như Hình 13.9.

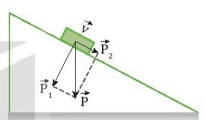
Hình 13.9

 

 

Phân tích lực là phép thay thế một lực bằng hai lực thành phần có tác dụng giống hệt lực đó.