1.1. Dấu của tam thức bậc hai
| Tam thức bậc hai (đối với x) là biểu thức có dạng ax2 + bx + c, trong đó a, b, c là những số thực cho trước (với \(a \ne 0\)), được gọi là các hệ số của tam thức bậc hai. |
|---|
Người ta thường viết f(x) = ax2 + bx + c. Các đa thức đã cho A = \(0,5x^{2}\), B = \(1-x^{2}\), C = \(x^{2}+x+1\), D = (1-x)(2x+1) là những tam thức bậc hai. Ở đa thức A, ta có ; a = 0,5; b = 0, c = 0.
Chú ý: Nghiệm của phương trình bậc hai ax2 + bx + c = 0 cũng được gọi là nghiệm của tam thức bậc hai ax2 + bx + c.

|
Cho tam thức bậc hai f(x) = ax2+ bx + c (\(a \ne 0\)). + Nếu \(\Delta < 0\) thì f(x) cùng dẫu với hệ số a với mọi \(x \in R\). + Nếu \(\Delta = 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \ne – \frac{b}{{2{\rm{a}}}}\) và \(f\left( { – \frac{b}{{2{\rm{a}}}}} \right) = 0\). + Nếu \(\Delta > 0\) thi tam thức f(x) có hai nghiệm phân biệt x1 và x2 \(\left( {{x_1} < {x_2}} \right)\). Khi đó f(x) cùng dấu với hệ số a với mọi \(x \in \left( { – \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\); f(x) trái dấu với hệ số a với mọi \(x \in \left( {{x_1};{x_2}} \right)\). |
|---|
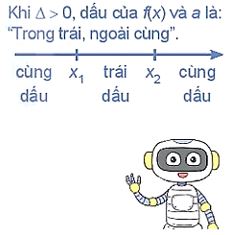
Chú ý: Trong Định lí về dấu tam thức bậc hai có thể thay \(\Delta \) bởi \(\Delta ‘\).
Ví dụ: Xét dâu các tam thức bậc hai sau:
\(\begin{array}{l}
a){x^2} + x + 1\\
b) – \frac{3}{2}{x^2} + 9x – \frac{{27}}{2}\\
c)2{x^2} + 6x – 8
\end{array}\)
Giải
a) \(f(x) = {x^2} + x + 1\) có \(\Delta = -3 < 0\) và a = 1 > 0 nên f(x) > 0 với mọi x \(\in\) R.
b) \(g(x) = – \frac{3}{2}{x^2} + 9x – \frac{{27}}{2}\) có \(\Delta = 0\) và \(a = – \frac{3}{2} > 0\) nên g(x) có nghiệm kép x = 3 và g(x) < 0 với mọi \(x \ne 3\).
c) Dễ thấy \(h(x) = 2{x^2} + 6x – 8\) có \(\Delta ‘ = 25 > 0,a = 2 > 0\) và có hai nghiệm phân biệt \({x_1} = – 4;{x_2} = 1\).
Do đó ta có bẳng xét dấu h(x)

Suy ra h(x) > 0 với mọi \(x \in \left( { – \infty ; – 4} \right) \cup \left( {1; + \infty } \right)\) và h(x) < 0 với mọi \(x \in \left( { – 4;1} \right)\).
1.2. Bất phương trình bậc hai
|
+ Bất phương trình bậc hai ẩn x là bất phương trình có dạng ax2+ bx + c > 0 (hoặc ax2+ bx + c > 0, ax2+ bx + c < 0, \(a{x^2} + bx + c \le 0\)), trong đó a, b, c là những số thực đã cho và \(a \ne 0\). + Số thực x0 gọi là một nghiệm của bất phương trình bậc hai ax2+ bx + c > 0, nếu ax2+ bx + c > 0. Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai ax2+ bx + c > 0 gọi là tập nghiệm của bắt phương trình này. + Giải bất phương trình bậc hai f(x)= ax2+ bx + c > 0 là tìm tập nghiệm của nó, tức là tìm các khoảng mà trong đó f(x) cùng dấu với hệ số a (nếu a > 0) hay trái dầu với hệ số a (nếu a < 0). |
|---|
Nhận xét: Để giải bất phương trình bậc hai ax2+ bx + c > 0 (hoặc \(a{x^2} + bx + c \ge 0\), ax2+ bx + c < 0, \(a{x^2} + bx + c \le 0\)) ta cần xét dấu tam thức ax2+ bx + c, từ đó suy ra tập nghiệm.
Ví dụ: Giải các bất phương trình sau:
\(\begin{array}{l}
a)3{x^2} + x + 5 \le 0\\
b) – 3{x^2} + 2\sqrt 3 – 1 \ge 0\\
c) – {x^2} + 2x + 1 > 0
\end{array}\)
Giải
a) Tam thức \(f(x) = 3{x^2} + x + 5\) có \(\Delta = – 59 < 0\), hệ số a = 3 > 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là \(3{x^2} + x + 5 > 0\) với mọi \(x \in R\). Suy ra bất phường trình vô nghiệm.
b) Tam thức \(f(x) = – 3{x^2} + 2\sqrt 3 – 1\) có \(\Delta ‘ = 0\), hệ số a = -3 < 0 nên f(x) luôn âm (cùng dấu với a) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\), tức là \(- 3{x^2} + 2\sqrt 3 – 1 < 0\) với mọi \(x = \frac{{\sqrt 3 }}{3}\).
Suy ra bất phương trình có nghiệm duy nhất \(x = \frac{{\sqrt 3 }}{3}\).
c) Tam thức \(f(x) = – {x^2} + 2x + 1\) có \(\Delta ‘ = 2 > 0\) nên f(x) có hai nghiệm \({x_1} = 1 – \sqrt 2 \) và \({x_2} = 1 + \sqrt 2 \)
Mặt khác a = -1 < 0, do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là \(S = \left( {1 – \sqrt 2 ;1 + \sqrt 2 } \right)\)