Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tuỳ ý và vẽ \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {BC}  = \overrightarrow b \) (Hình bên dưới). Khi đó vectơ \(\overrightarrow {AC} \) được gọi là tổng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a  + \overrightarrow b \).  Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

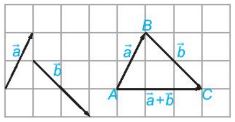
– Quy tắc ba điểm: Với ba điểm bắt kì A, B, C, ta có \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

– Quy tắc hình bình hành: Nếu ABCD là một hình binh hành thì \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \) 

– Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tuỳ ý:

• Tính chất giao hoán: \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \)
• Tính chất kết hợp: \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\)
• Tính chất của vectơ-không: \(\overrightarrow a  + \overrightarrow 0  = \overrightarrow 0  + \overrightarrow a  = \overrightarrow a \) 

Chú ý: Do các vectơ \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c \) và \(\overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\) bằng nhau, nên ta còn viết chúng dưới dạng \(\overrightarrow a  + \overrightarrow b  + \overrightarrow c \) và gọi là tổng cửa ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \). Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng các dấu ngoặc. 

Ví dụ: Cho hình Vuông ABCD với cạnh có độ dài bằng 1. Tính độ dài của các vectơ \(\overrightarrow {AB}  + \overrightarrow {CB} ,\overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BD} \). 

Giải

Do \(\overrightarrow {AB}  = \overrightarrow {DC} \) nên \(\overrightarrow {AB}  + \overrightarrow {CB}  = \overrightarrow {DC}  + \overrightarrow {CB}  = \overrightarrow {DB} \)

Vậy \(\left| {\overrightarrow {AB}  + \overrightarrow {CB} } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)

Ta có \(\overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BD}  = \left( {\overrightarrow {AB}  + \overrightarrow {BD} } \right) + \overrightarrow {DC}  = \overrightarrow {AD}  + \overrightarrow {DC}  = \overrightarrow {AC} \) 

Do đó \(\left| {\overrightarrow {AB}  + \overrightarrow {DC}  + \overrightarrow {BD} } \right| = AC = \sqrt 2 \) 

– Vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \). Vectơ đối của \(\overrightarrow a \) được kí hiệu là \(-\overrightarrow a \). – Vectơ \(\overrightarrow 0 \) được coi là vectơ đối của chính nó.

Chú ý: Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng \(\overrightarrow 0 \).

– Vectơ \(\overrightarrow a  + \left( { – \overrightarrow b } \right)\) được gọi là hiệu của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a  – \overrightarrow b \). Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

Chú ý: Nếu \(\overrightarrow b  + \overrightarrow c  = \overrightarrow a \) thì \(\overrightarrow a  – \overrightarrow b  = \overrightarrow a  + \left( { – \overrightarrow b } \right) = \overrightarrow c  + \overrightarrow b  + \left( { – \overrightarrow b } \right) = \overrightarrow c  + \overrightarrow 0  = \overrightarrow c \)

Với ba điểm O, M, N tuỷ ý, ta có \(\overrightarrow {MN}  = \overrightarrow {MO}  + \overrightarrow {ON}  = \left( { – \overrightarrow {OM} } \right) + \overrightarrow {ON}  = \overrightarrow {ON}  – \overrightarrow {OM} \)

– Quy tắc hiệu: Với ba điểm O, M, N, ta có \(\overrightarrow {MN}  = \overrightarrow {ON}  – \overrightarrow {OM} \)

Ví dụ: Cho hình bình hành ABCD và một điểm O bất kì.

Chứng minh rằng \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {OC}  – \overrightarrow {OD} \) 

Giải

Áp dụng quy tắc hiệu, ta có \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {AB} ,\overrightarrow {OC}  – \overrightarrow {OD}  = \overrightarrow {DC} \)

Mặt khác \(\overrightarrow {AB}  = \overrightarrow {DC} \) nên \(\overrightarrow {OB}  – \overrightarrow {OA}  = \overrightarrow {OC}  – \overrightarrow {OD} \)

Chú ý: Phép cộng vectơ tương ứng với các quy tắc tổng hợp lực, tổng hợp vận tốc:

+ Nếu hai lực cùng tác động vào chất điểm A và được biểu diễn bởi các vectơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) thì hợp lực tác động vào A được biểu diễn bởi vectơ \(\overrightarrow {{u_1}}  + \overrightarrow {{u_2}} \)

+ Nếu một con thuyền dĩ chuyển trên sông với vận tốc riêng (vận tốc so với dòng nước) được biểu diễn bởi vectơ \(\overrightarrow {{v_r}} \) và vận tốc của dòng nước (so với bờ) được biểu diễn bởi vectơ \(\overrightarrow {{v_n}} \) thì vận tốc thực tế của thuyền (so với bờ) được biểu diễn bởi vectơ \(\overrightarrow {{v_r}}  + \overrightarrow {{v_n}} \).