a. Thí nghiệm khảo sát chuyển động biến đổi

Mục đích: Đo được vận tốc tức thời tại từng thời điểm của vật chuyển động biến đổi.

Các dụng cụ và bố trí thí nghiệm như hình dưới đây:

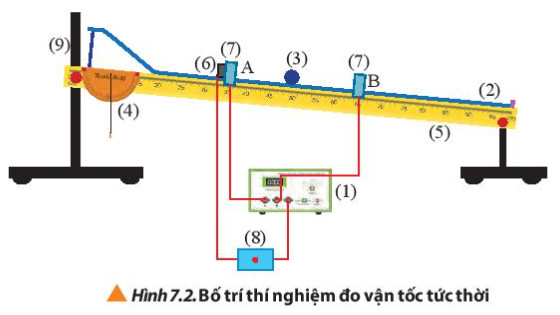
b. Gia tốc

– Đại lượng đặc trưng cho độ biến thiên của vật tốc theo thời gian được gọi là gia tốc. Trong chuyển động thẳng, gia tốc trung bình được xác định theo biểu thức: \({a_{tb}} = \frac{{\Delta v}}{{\Delta t}} = \frac{{{v_2} – {v_1}}}{{\Delta t}}\) – Gia tốc tức thời tại một thời điểm có giá trị bằng độ dốc của tiếp tuyến của đồ thị vận tốc – thời gian (v – t) tại thời điểm đó

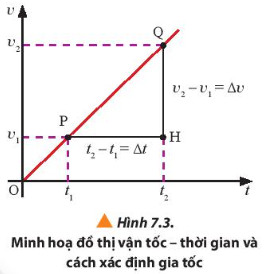
– Trong hệ SI, gia tốc có đơn vị là m/s²

– Do vận tốc là một đại lượng vecto nên gia tốc cũng là đại lượng vecto

– Gia tốc trung bình được xác định: 

\({\vec a_{tb}} = \frac{{\Delta \vec v}}{{\Delta t}} = \frac{{{{\vec v}_2} – {{\vec v}_1}}}{{\Delta t}}\)

– Dựa vào giá trị của gia tốc tức thời để phân chuyển động thành những loại sau:

+ a = 0: chuyển động thẳng đều, vật có độ lớn vận tốc không đổi.

+ a ≠ 0 và bằng hằng số: chuyển động thẳng biến đổi đều, vật có độ lớn vật tốc thay đổi (tăng hoặc giảm) đều theo thời gian.

+ a ≠ 0 nhưng không phải hằng số: chuyển động thẳng biến đổi phức tạp.

c. Vận dụng đồ thị (v – t) xác định độ dịch chuyển

Độ dịch chuyển của vật trong khoảng thời gian từ t1 đến t2 được xác định bằng phần diện tích giới hạn bởi các đường v(t), v = 0, t = t1, t = t2 trong đồ thị (v – t)

Ví dụ:

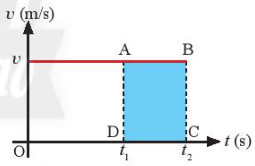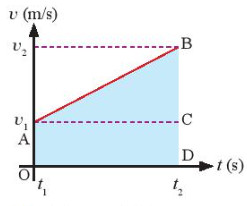Chuyển động thẳng đều	Chuyển động thẳng biến đổi đều

a. Các phương trình của chuyển động thẳng biến đổi đều

– Phương trình gia tốc: a = hằng số

– Phương trình vận tốc: v = v_o + a.t (do chọn t₀ = 0)

– Phương trình độ dịch chuyển: \(d = \frac{1}{2}a.{t^2} + {v_o}.t\)

– Phương trình xác định tọa độ của vật chuyển động thẳng biến đổi đều không đổi chiều: \(x = \frac{1}{2}a.{t^2} + {v_o}.t + {x_o}\)

– Phương trình liên hệ giữa gia tốc, vận tốc và độ dịch chuyển: \({v^2} – v_o^2 = 2a.d\)

– Đồ thị (d – t) của chuyển động thẳng biến đổi đều được biểu diễn là một nhánh parabol

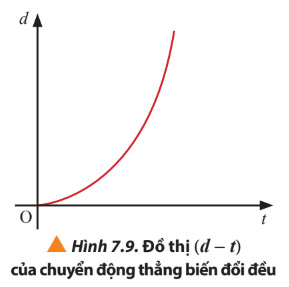
b. Vận dụng các công thức của chuyển động thẳng biến đổi đều

– Ví dụ 1: 

Một người đi xe đạp lên dốc dài 50 m. Tốc độ ở dưới chân dốc là 18 km/h và ở đầu dốc lúc đến nơi là 3 m/s. Tính gia tốc của chuyển động và thời gian lên dốc. Coi chuyển động trên là chuyển động thẳng chậm dần đều.

Hướng dẫn giải:

Chọn gốc thời gian là lúc vật ở chân dốc, chiều dương cùng chiếu chuyển động.

Áp dụng phương trình, suy ra:

\(a = \frac{{{v^2} – v_o^2}}{{2.d}} = \frac{{{3^2} – {{\left( {18/3.,} \right)}^2}}}{{2.50}} =  – 0,16m/{s^2}\)

Thời gian chuyển động lên dốc:

\(t = \frac{{v – {v_0}}}{a} = \frac{{3 – 5}}{{ – 0,16}} = 12,5s\)

Như vây, gia tốc có độ lớn không đổi bằng 0,16m/s² và có chiều ngược chiều dương theo quy ước là chiều chuyển động, do đó vật chuyển động chậm dần đều

– Ví dụ 2: Một người đi xe đạp chuyển động thẳng nhanh dần đều (như hình 7.10). Trong hai khoảng thời gian 4s liên tiếp, người này di chuyển được những quãng đường lần lượt là 24m và 64m. Tính gia tốc và tốc độ ban đầu của chuyển động.

Hướng dẫn giải:

Chọn gốc thời gian lúc bắt đầu chuyển động, chiều dương cùng chiều chuyển động.

Ta có:

t₁=4s; d₁=s₁=24m

t₂=8s;d₂=s₁+s₂=88m

Thay vào phương trình độ dịch chuyển theo thời gian và giải hệ phương trình, ta có:

\(\left\{ \begin{array}{l}
{v_0} = 1m/s\\
a = 2,5m/{s^2}
\end{array} \right.\)