1.1. Đạo hàm của một số hàm sơ cấp cơ bản
a. Đạo hàm của hàm số \(y={{x}^{n}}(n\in N,n>1)\)
| Hàm số \(y={{x}^{n}}(n\in N,n>1)\) có đạo hàm tại mọi \(x \in R\) và \(({{x}^{n}})’ =n{{x}^{n-1}}\). |
Nhận xét: Bằng định nghĩa, ta chứng minh được:
– Đạo hàm của hàm hằng bằng 0: (c)’ = 0 với c là hằng số.
– Đạo hàm của hàm số y = x bằng 1: (x)’ = 1.
b. Đạo hàm của hàm số \(y=\sqrt x\)
|
Hàm số \(y=\sqrt x\) có đạo hàm tại mọi \(x \in R, x>0\) và \((\sqrt x)’={1 \over {2 \sqrt x}}\). |
c. Đạo hàm của hàm số lượng giác
|
– Hàm số \(y = sin x\) có đạo hàm tại mọi \(x \in R\) và \((sinx)’ = cosx\). – Hàm số \(y = cos x\) có đạo hàm tại mọi \(x \in R\) và \((cosx)’ = – sinx\). – Hàm số \(y = tan x\) có đạo hàm tại mọi \(x\ne \frac{\pi }{2}+k\pi ,k\in Z\) và \((\tan x)’=\frac{1}{{{\cos }^{2}}x}\). – Hàm số \(y = cot x\) có đạo hàm tại mọi \(x\ne k\pi ,k\in Z\) và \((\cot x)’=\frac{1}{{{\sin }^{2}}x}\). |
d. Đạo hàm của hàm số mũ
|
– Hàm số \(y = {{e}^{x}}\) có đạo hàm tại mọi \(x \in R\) và \(({{e}^{x}})’ ={{e}^{x}}\). – Hàm số \(y = {{e}^{x}}\) \((a > 0, a \ne 1)\) có đạo hàm tại mọi \(x \in R\) và \(({{a}^{x}})’ ={{e}^{x}}lna\). |
e. Đạo hàm của hàm số lôgarit
|
– Hàm số \(y = ln x\) có đạo hàm tại mọi x dương và \((lnx)’ = {{1}^{x}}\) – Hàm số \(y = {log_a}x\) \((a>0, a \ne 1)\) có đạo hàm tại mọi x dương và \(({log_a}x)’=1 \over xlna\). |
1.2. Đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp
a. Đạo hàm của tổng, hiệu, tích, thương
Định lí
|
Giả sử \(f = f(x), g = g(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có: \((f+g)’=f’+g’\) \((fg)’= f’g+fg’\) \((f-g)’=f’-g’\) \(\left( \frac{f}{g} \right)’=\frac{f’g-fg’}{{{g}^{2}}}(g=g(x)\ne 0)\) |
Hệ quả: Cho \(f = f(x)\) là hàm số có đạo hàm tại điểm x thuộc khoảng xác định.
– Nếu c là một hằng số thì \((cf)’ = cf’\).
– \(\left( \frac{1}{f} \right)’=-\frac{f’}{{{f}^{2}}}(f=f(x)\ne 0)\).
b. Đạo hàm của hàm hợp
Giả sử hàm số \(u = g(x)\) xác định trên (a ; b) và lấy giá trị trên (c ; d); \(y = f(u)\) là hàm số của u, xác định trên (c ; d) và lấy giá trị trên R. Khi đó, ta có thể lập được một hàm số mới xác định trên (a ; b) và lấy giá trị trên R theo quy tắc như hình dưới.
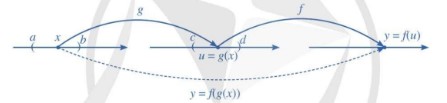
Hàm số \(y = f(g(x))\) được gọi là hàm hợp của hai hàm số \(y=f(u), u=g(x)\).
Quy tắc tính đạo hàm của hàm hợp
| Nếu hàm số \(u = g(x)\) có đạo hàm tại x là \({u’_x}\) và hàm số \(y = f(u)\) có đạo hàm tại u là \({y’_u}\) thì hàm hợp \(y = f(g(x))\) có đạo hàm tại x là ({y’_x}={y’_u}.{u’_x}\). |
Nhận xét: Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp:
