1.1. Hàm số mũ
a. Định nghĩa
| Cho số thực a \((a > 0, a \ne 1)\). Hàm số \(y = {{a}^{x}}\) được gọi là hàm số mũ cơ số a. |
Tập xác định của hàm số mũ \(y = {{a}^{x}}\) \((a > 0, a \ne 1)\) là R.
b. Đồ thị và tính chất
Tổng quát
| Đồ thị hàm số \(y = {{a}^{x}}\) \((a > 0, a \ne 1)\) là một đường cong liền nét, cắt trục tung tại điểm có tung độ bằng 1, nằm ở phía trên trục hoành và đi lên nếu \(a > 1\), đi xuống nếu \(0 |
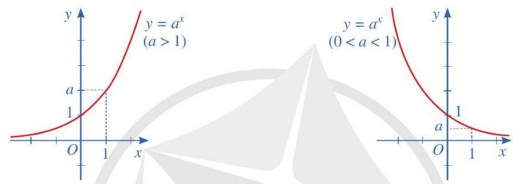
Nhận xét: Cho hàm số mũ \(y = {{a}^{x}}\) \((a > 0, a \ne 1)\).

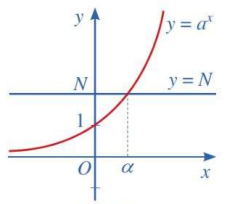
Chú ý: Từ tính liên tục và sự biến thiên của hàm số mũ, ta có thể chứng minh được mệnh đề sau:
Với mỗi N > 0, đường thẳng y = N cắt đồ thị hàm số mũ \(y = {{a}^{x}}\) \((a > 0, a \ne 1)\) tại một và chỉ một điểm. Nói cách khác, ta có: Với mỗi N > 0, tồn tại duy nhất số thực a sao cho \({{a}^{ \alpha}} = N\).
1.2. Hàm số lôgarit
a. Định nghĩa
| Cho số thực a \((a > 0, a \ne 1)\). Hàm số \(y=lo{{g}_{a}}x\) được gọi là hàm số lôgarit cơ số a. |
Tập xác định của hàm số lôgarit \(y=lo{{g}_{a}}x\) \((a > 0, a \ne 1)\) là \((0;+\infty )\).
b. Đồ thị và tính chất
Tổng quát
|
Đồ thị hàm số\(y=lo{{g}_{a}}x\) \((a > 0, a \ne 1)\) là một đường cong liền nét, cắt trục hoành tại điểm có hoành độ bằng 1, nằm ở phía bên phải trục tung và đi lên nếu \(a > 1\), đi xuống nếu \(0 < a < 1\). |
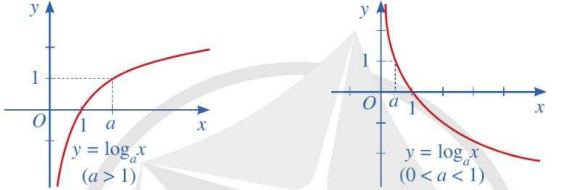
Nhận xét: Cho hàm số lôgarit \(y=lo{{g}_{a}}x\) \((a > 0, a \ne 1)\).
