Định nghĩa

Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu \(\Omega \). Đặt \(C=A\cup B\), ta có C là một biến cố và được gọi là biến cố hợp của hai biến cố A và B, kí hiệu là \(A\cup B\).

Chú ý:

Xét một kết quả thuận lợi \(\alpha \) cho biến cố C, tức là \(\alpha \in C\). Vì \(C=A\cup B\) nên  \(\alpha \in A\) hoặc \(\alpha \in B\). Nói cách khác, \(\alpha \) là một kết quả thuận lợi cho biến cố A hoặc biến cố B. Điều đó có nghĩa là biến cố A hoặc biến cố B xảy ra. Vì vậy, biến cố C có thể phát biểu dưới dạng mệnh đề nêu sự kiện là “A xảy ra hoặc B xảy ra” hay “Có ít nhất một trong các biến cố A, B xảy ra”.

 

Định nghĩa

Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu \(\Omega \). Đặt \(D=A\cap B\), ta có D là một biến cố và được gọi là biến cố giao của hai biến cố A và B, kí hiệu là \(A\cap B\) hay AB.

Chú ý:

Xét một kết quả thuận lợi \(\beta \) cho biến cố D, tức là \(\beta \in D\). Vì \(D=A\cap B\) nên \(\beta \in A\); \(\beta \in B\). Nói cách khác, \(\beta \) là một kết quả thuận lợi cho cả hai biến cố A và B. Điều đó có nghĩa là cả hai biến cố A và B cùng xảy ra. Vì vậy, biến cố D có thể phát biểu dưới dạng mệnh đề nêu sự kiện là “Cả A và B cùng xảy ra”.

 

Định nghĩa

Cho hai biến cố A và B. Khi đó A, B là các tập con của không gian mẫu \(\Omega \). Nếu \(A\cap B=\varnothing \) thì A và B gọi là hai biến cố xung khắc.

Chú ý:

Xét một kết quả thuận lợi \(\gamma \) cho biến cố A, tức là \(\gamma \in A\). Vì \(A\cap B=\varnothing \) nên \(\gamma \notin B\), tức là \(\gamma \) không là một kết quả thuận lợi cho biến cố B. Do đó, hai biến cố A và B là xung khắc khi và chỉ khi nếu biến cố này xảy ra thì biến cố kia không xảy ra.

 

Định nghĩa

Cho hai biến cố A và B. Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia.

Chú ý:

Nếu A, B là hai biến cố độc lập thì mỗi cặp biến cố sau cũng độc lập:

\(A\) và \(\overline{B}\); \(\overline{A}\) và \(B\); \(\overline{A}\) và \(\overline{B}\)

 

Định lí

Cho hai biến cố A và B. Khi đó \(P\left( A\cup B \right)=P(A)+P(B)-P\left( A\cap B \right)\).

– Nếu hai biến cố A và B là xung khắc thì \(A\cap B=\varnothing \), suy ra \(P\left( A\cap B \right)=0\). Vì thế, ta có hệ quả sau:

Hệ quả:  Nếu hai biến cố A và B là xung khắc thì \(P\left( A\cup B \right)=P(A)+P(B)\).

 

Định lí

– Cho hai biến cố A và B.  – Nếu hai biến cố A và B là độc lập thì \(P\left( A\cap B \right)=P(A).P(B)\).

Chú ý:

Nếu \(P\left( A\cap B \right)\ne P(A).P(B)\) thì hai biến cố A và B không độc lập.

 

Ví dụ: Một đội văn nghệ có 4 học sinh nam và 5 học sinh nữ. Giáo viên phụ trách đội muốn chọn ra một đội tốp ca gồm 3 học sinh sao cho có cả nam và nữ cùng tham gia.

a) Giáo viên phụ trách đội có bao nhiêu cách chọn một đội tốp ca như vậy?

b) Tính xác suất của biến cố H: “Trong 3 học sinh chọn ra có cả nam và nữ”. 

 

Hướng dẫn giải

– Xét các biến cố:

H: “Trong 3 học sinh chọn ra có cả nam và nữ;

A: “Trong 3 học sinh chọn ra có 2 học sinh nam và 1 học sinh nữ”;

B: “Trong 3 học sinh chọn ra có 1 học sinh nam và 2 học sinh nữ”.

– Khi đó \(H=A\cup B\) và \(A\cap B=\varnothing \).

Do hai biến cố A và B là xung khắc nên \(n(H)=n(A)+n(B)\).

a) Số các kết quả thuận lợi cho biến cố A là:

\(n(A)=C_{4}^{2}.C_{5}^{1}=\frac{4!}{2!.2!}.\frac{5!}{1!.4!}=6.5=30\)

Số các kết quả thuận lợi cho biến cố B là:

\(n(B)=C_{4}^{1}.C_{5}^{2}=\frac{4!}{1!.3!}.\frac{5!}{2!.3!}=4.10=40\)

Số các kết quả thuận lợi cho biến cố H là:

\(n(H)=n(A)+n(B)=30+40=70\)

Vậy giáo viên phụ trách có 70 cách chọn một đội tốp ca như dự định.

b) Đội văn nghệ có 9 học sinh. Mỗi cách chọn 3 học sinh trong 9 học sinh đó là một tổ hợp chập 3 của 9 phần tử. Do đó, không gian mẫu S2 gồm các tổ hợp chập 3 của 9 phần tử và

\(n(\Omega )=C_{9}^{3}=\frac{9!}{3!.6!}=84\)

Vậy xác suất của biến cố H là: 

\(P(H)=\frac{n(H)}{n(\Omega )}=\frac{70}{84}=\frac{5}{6}\)

 

Ví dụ: Câu lạc bộ nghệ thuật của một trường trung học phổ thông gồm học sinh của cả ba khối 10, 11, 12, mỗi khối có 5 học sinh. Chọn ngẫu nhiên 3 học sinh để tham gia biểu diễn. Tính xác suất để 3 học sinh được chọn chỉ thuộc hai khối.

 

Hướng dẫn giải

– Mỗi cách chọn ra đồng thời 3 học sinh trong câu lạc bộ cho ta một tổ hợp chập 3 của 15 phần tử. Do đó, không gian mẫu \(\Omega \) gồm các tổ hợp chập 3 của 15 phần tử và

\(n(\Omega )=C_{15}^{3}=\frac{15!}{3!.12!}=455\)

– Xét biến cố A: “Chọn được 3 học sinh chỉ thuộc hai khối”.

 

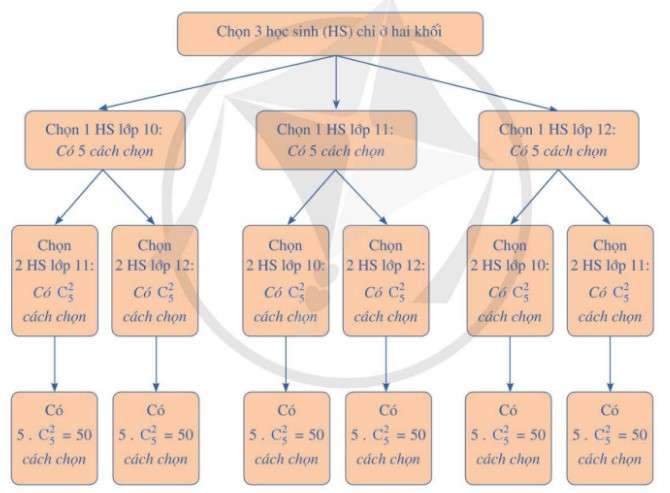
Sơ đồ hình cây biểu thị các khả năng thuận lợi cho biến cố A

 

Như vậy, số kết quả thuận lợi cho biến cố A là: n(A) = 50.6 = 300.

Vậy xác suất của biến cố A là: \(P(A)=\frac{n(A)}{n(\Omega )}=\frac{300}{455}=\frac{60}{91}\)