1.1. Mẫu số liệu ghép nhóm
a. Bảng tần số ghép nhóm
|
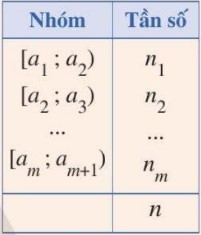
– Mẫu số liệu ghép nhóm là mẫu số liệu cho dưới dạng bảng tần số ghép nhóm. – Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng [a; b), trong đó a là đầu mút trái, b là đầu mút phải. Độ dài nhóm là b – a. – Tần số của một nhóm là số số liệu trong mẫu số liệu thuộc vào nhóm đó. Tần số của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là \({{n}_{1}},{{n}_{2}},…,{{n}_{m}}\). – Bảng tần số ghép nhóm được lập như ở Bảng bên dưới, trong đó mẫu số liệu gồm n số liệu được chia thành m nhóm ứng với m nửa khoảng \(({{a}_{1}};{{a}_{2}});({{a}_{2}};{{a}_{3}});…;({{a}_{m}};{{a}_{m+1}})\), ở đó: \({{a}_{1}}<{{a}_{2}}<…<{{a}_{m}}<{{a}_{m+1}}\) và \(n={{n}_{1}}+{{n}_{2}}+…+{{n}_{m}}\) |
b. Ghép nhóm số liệu. Tần số tích luỹ
|
Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta thực hiện như sau: – Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước. – Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng tần số ghép nhóm. |
Chú ý: Khi ghép nhóm số liệu, ta thường phân chia các nhóm có độ dài bằng nhau và đầu mút của các nhóm có thể không phải là giá trị của mẫu số liệu. Nhóm cuối cùng có thể là \([{{a}_{m}};{{a}_{m+1}}]\).
Định nghĩa
|
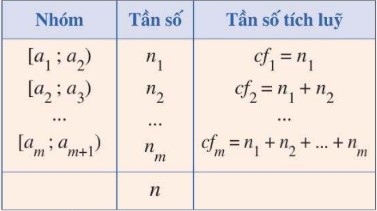
– Tần số tích luỹ của một nhóm là số số liệu trong mẫu số liệu có giá trị nhỏ hơn giá trị đầu mút phải của nhóm đó. Tần số tích luỹ của nhóm 1, nhóm 2, …, nhóm m kí hiệu lần lượt là \(c{{f}_{1}},c{{f}_{2}},…,c{{f}_{m}}\). – Bảng tần số ghép nhóm bao gồm cả tần số tích luỹ được lập như ở Bảng bên dưới. |
1.2. Số trung bình cộng (số trung bình)
Định nghĩa
|
– Trung điểm \({{x}_{i}}\) của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm i là giá trị đại diện của nhóm đó. – Số trung bình cộng của mẫu số liệu ghép nhóm, kí hiệu \(\overline{x}\), được tính theo công thức: \(\overline{x}=\frac{{{n}_{1}}{{x}_{1}}+{{n}_{2}}{{x}_{2}}+…+{{n}_{m}}{{x}_{m}}}{n}\) |
Ý nghĩa
– Số trung bình cộng của mẫu số liệu không ghép nhóm là giá trị trung bình cộng của các số trong mẫu số liệu đó, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu khi các số liệu trong mẫu ít sai lệch với số trung bình cộng.
– Số trung bình cộng của mẫu số liệu sau khi ghép nhóm xấp xỉ với số trung bình cộng của mẫu số liệu không ghép nhóm ban đầu và có thể làm đại diện cho vị trí trung tâm của mẫu số liệu.
1.3. Trung vị
Định nghĩa
Giả sử nhóm k là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{2}\),tức là \(c{{f}_{k-1}}<\frac{n}{2}\) nhưng \(c{{f}_{k}}\ge \frac{n}{2}\).Ta gọi \(r,d,{{n}_{k}}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm k; \(c{{f}_{k-1}}\) là tần số tích luỹ của nhóm k − 1.
|
Trung vị của mẫu số liệu ghép nhóm, kí hiệu \({{M}_{e}}\), được tính theo công thức sau: \({{M}_{e}}=r+\left( \frac{\frac{n}{2}-c{{f}_{k-1}}}{{{n}_{k}}} \right).d\) |
Trung vị của mẫu số liệu sau khi ghép nhóm xấp xỉ với trung vị của mẫu số liệu không
ghép nhóm ban đầu và có thể dùng để đại diện cho mẫu số liệu đã cho.
1.4. Tứ phân vị
Định nghĩa
| Tứ phân vị thứ hai \({{Q}_{2}}\), bằng trung vị \({{M}_{e}}\). |
– Giả sử nhóm p là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4}\), tức là \(c{{f}_{p-1}}<\frac{n}{4}\) nhưng \(c{{f}_{p}}\ge \frac{n}{4}\). Ta gọi \(s,h,{{n}_{p}}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(p,c{{f}_{p-1}}\) là tần số tích luỹ của nhóm p − 1.
|
Tứ phân vị thứ nhất \({{Q}_{1}}\), được tính theo công thức sau: \({{Q}_{1}}=s+\left( \frac{\frac{n}{4}-c{{f}_{p-1}}}{{{n}_{p}}} \right).h\) |
– Giả sử nhóm q là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{3n}{4}\) ,tức là \(c{{f}_{q-1}}<\frac{3n}{4}\) nhưng \(c{{f}_{q-1}}\ge \frac{3n}{4}\).Ta gọi \(t,l,{{n}_{q}}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm q; là tần số tích luỹ của nhóm q − 1.
|
Tứ phân vị thứ ba \({{Q}_{3}}\),được tính theo công thức sau: \({{Q}_{3}}=t+\left( \frac{\frac{3n}{4}-c{{f}_{q-1}}}{{{n}_{q}}} \right).l\) |
– Đối với mẫu số liệu không ghép nhóm đã sắp xếp theo thứ tự từ nhỏ đến lớn, các điểm \({{Q}_{1}},{{Q}_{2}},{{Q}_{3}}\) chia mẫu số liệu đó thành bốn phần, mỗi phần đều chứa 25% giá trị.
– Bằng cách ghép nhóm mẫu số liệu và tính toán tứ phân vị của mẫu số liệu ghép nhóm, ta nhận được ba giá trị mới cũng có thể dùng để đại diện cho mẫu số liệu đã cho.
Lưu ý: Bộ ba giá trị \({{Q}_{1}},{{Q}_{2}},{{Q}_{3}}\) trong tứ phân vị của mẫu số liệu sau khi ghép nhóm xấp xỉ với bộ ba giá trị trong tứ phân vị của mẫu số liệu không ghép nhóm ban đầu.
1.5. Mốt
Định nghĩa
Giả sử nhóm i là nhóm có tần số lớn nhất. Ta gọi \(u,g,{{n}_{i}}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(i,{{n}_{i-1}},{{n}_{i+1}}\) lần lượt là tần số của nhóm i – 1, nhóm i + 1.
|
Mốt của mẫu số liệu ghép nhóm, kí hiệu \({{M}_{o}}\), được tính theo công thức sau: \({{M}_{o}}=u+\left( \frac{{{n}_{i}}-{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i-1}}-{{n}_{i+1}}} \right).g\) |
Chú ý:
– Khi i = 0 thì \({{n}_{o}}=0\).
– Khi i = m thì \({{n}_{m+1}}=0\).
Ý nghĩa
– Mốt của một mẫu số liệu không ghép nhóm đặc trưng cho số lần lặp đi lặp lại nhiều nhất tại một giá trị của mẫu số liệu đó. Vì thế, có thể dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu số liệu có nhiều giá trị trùng nhau.
– Bằng cách ghép nhóm mẫu số liệu và tính toán mốt của mẫu số liệu ghép nhóm, ta nhận được giá trị mới cũng có thể dùng để đo xu thế trung tâm của mẫu số liệu đã cho.
– Mốt của mẫu số liệu sau khi ghép nhóm xấp xỉ với mốt của mẫu số liệu không ghép nhóm ban đầu. Một mẫu số liệu ghép nhóm có thể có nhiều mốt.