1.1. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
a. Hàm số chẵn, hàm số lẻ
|
Cho hàm số \(y = f(x)\) với tập xác định D. Hàm số \(y = f(x)\) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( – x \in D\) và \(f( – x) = f(x)\). Hàm số \(y = f(x)\) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( – x \in D\) và \(f( – x) = f(x)\). |
– Chú ý:
Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
Đồ thị hàm số lẻ nhận góc toạ độ làm tâm đối xứng.
b. Hàm số tuần hoàn
|
Cho hàm số \(y = f(x)\) với tập xác định D. Hàm số \(y = f(x)\) được gọi là tuần hoàn nếu tồn tại một số T khác 0 sao cho \(\forall x \in D\), ta có:
Số T dương nhỏ nhất thoả mãn (nếu có) các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó. |
– Nhận xét:
Cho hàm số tuần hoàn chu kì T. Từ đồ thị hàm số đó trên đoạn [a; a+T], ta dịch chuyển song song với trục hoành sang phải (hoặc sang trái) theo đoạn có độ dài T thì được đồ thị hàm số trên đoạn [a+T; a+2T] (hoặc [a-T; a]).
1.2. Hàm số \(y = \sin x\)
a. Định nghĩa
| Quy tắc đặt tương ứng mỗi số thực x với một số thực sinx được gọi là hàm số
\(y = \sin x\). Tập xác định của hàm số \(y = \sin x\) là \(ℝ\). |
b. Đồ thị của hàm số \(y = \sin x\)
– Đồ thị hàm số \(y = \sin x\) trên \(ℝ\) được biểu diễn như sau:
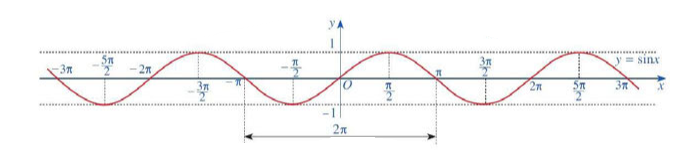
c. Tính chất của hàm số y = sinx
|
Hàm số \(y = \sin x\) là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O. Hàm số\(y = \sin x\) tuần hoàn chu kì \(2\pi \). Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( {\frac{{ – \pi }}{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{{ \pi }}{2} + k2\pi ;\frac{3pi }{2} + k2\pi } \right)\) với \(k \in ℤ\). |
– Nhận xét: Dựa vào đồ thị của hàm số \(y = \sin x\), ta thấy \(\sin x = 0\) tại những giá trị \(x = k\pi (k \in ℤ\). Vì vậy, tập hợp các số thực x sao cho \(\sin x \ne 0\) là \(E{\rm{ }} =ℝ \backslash \{ k\pi |k \in ℤ\} \).
1.3. Hàm số \(y = \cos x\)
a. Định nghĩa
|
Quy tắc đặt tương ứng mỗi số thực x với một số thực cosx được gọi là hàm số \(y = \cos x\). Tập xác định của hàm số \(y = \cos x\) là ℝ. |
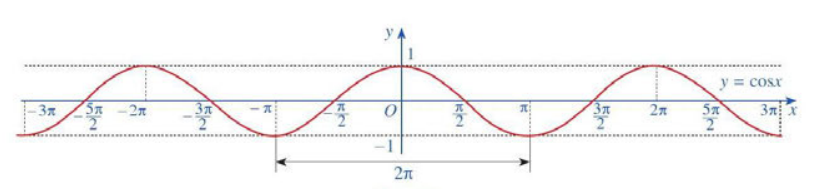
b. Đồ thị của hàm số \(y = \cos x\)
c. Tính chất của hàm số \(y = \cos x\)
|
Hàm số \(y = \cos x\) là hàm số chẵn, có đồ thị đối xứng qua trục tung. Hàm số \(y = \cos x\) tuần hoàn chu kì \(2\pi \). Hàm số \(y = \cos x\) đồng biến trên mỗi khoảng \(( – \pi + k2\pi ;k2\pi )\), nghịch biến trên mỗi khoảng \((k2\pi ;\pi + k2\pi )\) với \(k \in \)ℤ. |
– Nhận xét: Dựa vào đồ thị của hàm số \(y = \cos x\), ta thấy cosx = 0 tại những giá trị \(x = \frac{\pi }{2} + k\pi (k \in ℤ\). Vì vậy, tập hợp các số thực x sao cho \(\cos x \ne 0\) là \(D = ℝ\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in ℤ} \right\}\).
1.4. Hàm số \(y = \tan x\)
a. Định nghĩa
| Quy tắc đặt tương ứng mỗi số thực x với một số thực tanx được gọi là hàm số
\(y = \tan x\). Tập xác định của hàm số \(y = \tan x\) là \(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in Z} \right\}\). |
b. Đồ thị của hàm số \(y = \tan x\)
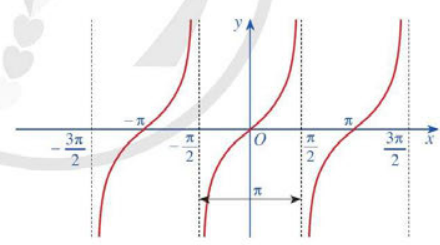
c. Tính chất của hàm số \(y = \tan x\)
|
Hàm số \(y = \tan x\) là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O. Hàm số \(y = \tan x\) tuần hoàn chu kì . Hàm số \(y = \tan x\) đồng biến trên mỗi khoảng \(\left( {\frac{{ – \pi }}{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với \(k \in \)ℤ. |
1.5. Hàm số \(y = \cot x\)
a. Định nghĩa
|
Quy tắc đặt tương ứng mỗi số thực x với một số thực cotx được gọi là hàm số \(y = \cot x\). Tập xác định của hàm số \(y = \cot x\) là \(E = R\backslash \left\{ {k\pi |k \in Z} \right\}\). |
b. Đồ thị của hàm số \(y = \cot x\)
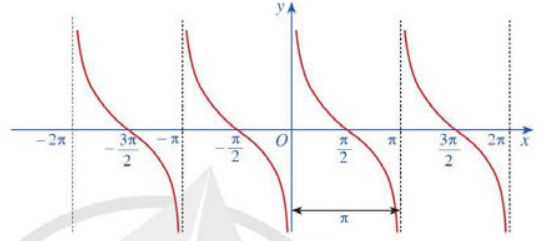
c. Tính chất của hàm số \(y = \cot x\)
|
Hàm số \(y = \cot x\) là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O. Hàm số \(y = \cot x\) tuần hoàn chu kì π. Hàm số \(y = \cot x\) nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\), với \(k \in \)ℤ. |