1.1. Góc lượng giác

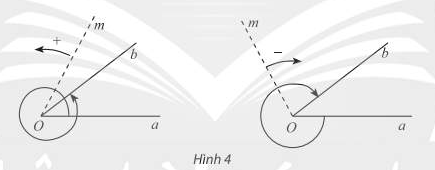
Khi xét chuyển động quay của một tia Om ta quy ước: Chiều quay ngược với chiều quay của kim đồng hồ là chiều dương, chiều quay cùng chiều kim đồng hồ là chiều âm.

Cho hai tia Oa, Ob. – Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob, kí hiệu (Oa, Ob). – Khi tia Om quay một góc \(\alpha\), ta nói số đo của góc lượng giác (Oa, Ob) bằng \(\alpha\), kí hiệu sđ(Oa, Ob) = \(\alpha\).

 

 

Chú ý: Với hai tia Oa và Ob cho trước, có vô số góc lượng giác tia đầu Oa và tia cuối Ob.

Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.

Nhận xét: Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai khác nhau một bội nguyên của 360° nên có công thức tổng quát là:

sđ(Oa , Ob) = \(\alpha ^0\) +k 360\(^0\) (k ∈ Z)

với \(\alpha ^0\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.

 

Ta thừa nhận hệ thức sau: gọi là Hệ thức Chasles:

Với ba tia Oa, Ob, Oc bất kì, ta có sđ(Oa, Ob) + sđ(Ob, Oc) = sđ(Oa,Oc) + k360° (k ∈ Z).

1.2. Đơn vị radian

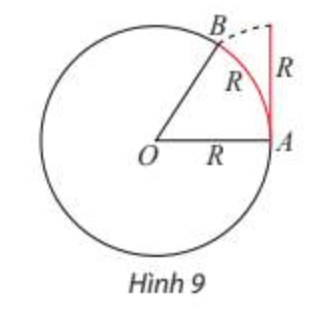
Trên đường tròn bán kính R tuỳ ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (đọc là 1 ra-đi-an, viết tắt là 1 rad).

 

Trên đường tròn bán kính R, một góc ở tâm có số đo \(\alpha\) rad thì chắn một cung có độ dài \(\alpha\)R (Hình 10).

 

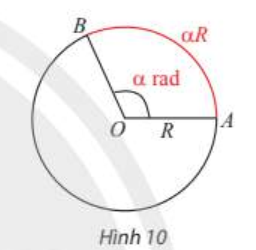
Công thức chuyển đổi số đo góc từ đơn vị radian sang độ và ngược lại:

\(a\)° = \(\pi a\over 180\)  rad và \(\alpha\) rad = \({180 \alpha\over \pi}^°\)

 

Chú ý: 

+ Khi viết số đo của một góc theo đơn vị radian, người ta thường không viết chữ rad sau số đo.

+ Với đơn vị radian, công thức số đo tổng quát của góc lượng giác (Oa, Ob) là

(Оa, Ob) = \(\alpha\) + k2π (k ∈ Z).

trong đó \(\alpha\) là số đo theo radian của một góc lượng giác bất kẻ có tia đầu Oa và tia cuối Ob.

 Lưu ý: không được viết \(\alpha\) + k360° hay a° +k2π (vì không cùng đơn vị đo).

 

1.3. Đường tròn lượng giác

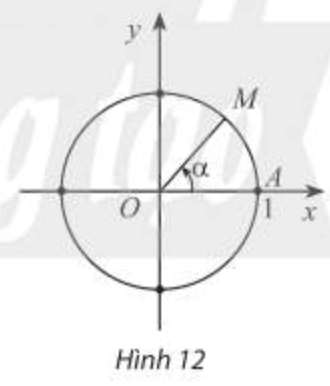
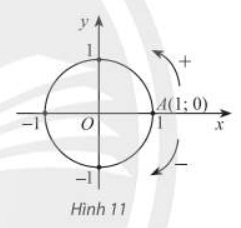
Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm O bán kính bằng 1. Trên đường tròn này, chọn điểm A(1;0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là chiều cùng chiều kim đồng hồ.   Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác.

 

Cho số đo góc \(\alpha\) bất kì. Trên đường tròn lượng giác, ta xác định được duy nhất một điểm M sao cho số do góc lượng giác (OA, OM) bằng \(\alpha\) (Hình 12). Khi đó điểm M được gọi là điểm biểu diễn của góc có số đo ở trên đường tròn lượng giác.